
分析 (1)求出f′(x),因为函数在x=1处取得极值,在x=-1处的切线斜率为2,联立方程组解得a与b的值,然后把a、b的值.
(2)判断函数的单调性,由于x∈[-1,2]恒成立求出函数的最大值值为f(2),代入求出最大值,然后令f(2)<c2列出不等式,求出c的范围即可.
解答 解:(1)f(x)=x3+ax2+bx+c,f'(x)=3x2+2ax+b,
由$\left\{\begin{array}{l}{f′(1)=3+2a+b=0}\\{f′(-1)=3-2a+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-2}\end{array}\right.$,
(2)由(1)可得:f'(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
| x | (-∞,-$\frac{2}{3}$) | -$\frac{2}{3}$ | (-$\frac{2}{3}$,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
点评 考查学生利用导数研究函数极值的能力,利用导数研究函数单调性的能力,以及理解函数恒成立时所取到的条件.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
选修4—4:坐标系与参数方程
已知曲线C1的参数方程为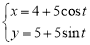 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 .
.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标( ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
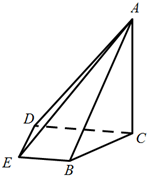 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com