
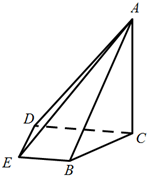 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.分析 (1)依题意,易证AC⊥平面BCDE,于是可得AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;
(2)作BF⊥AD,与AD交于点F,BO⊥CD,与CD交于点O,连接OF,由(1)知OF⊥AD,所以∠BFO就是二面角B-AD-C的平面角,即可求出二面角B-AD-C的正切值.
解答 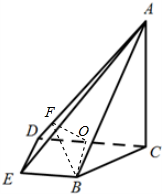 (1)证明:在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=$\sqrt{2}$,
(1)证明:在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=$\sqrt{2}$,
由AC=$\sqrt{2}$,AB=2得AB2=AC2+BC2,即AC⊥BC,
又平面ABC⊥平面BCDE,从而AC⊥平面BCDE,
所以AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;
(2)解:作BF⊥AD,与AD交于点F,BO⊥CD,与CD交于点O,连接OF,
由(1)知OF⊥AD,所以∠BFO就是二面角B-AD-C的平面角,
在直角梯形BCDE中,由CD2=BC2+BD2,得BD⊥BC,
又平面ABC⊥平面BCDE,得BD⊥平面ABC,从而BD⊥AB,
由于AC⊥平面BCDE,得AC⊥CD.
在Rt△ACD中,由DC=2,AC=$\sqrt{2}$,得AD=$\sqrt{6}$;
在Rt△ABD中,由BD=$\sqrt{2}$,AB=2,AD=$\sqrt{6}$得BF=$\frac{2\sqrt{3}}{3}$,
BO=DE=1,∴OF=$\frac{\sqrt{3}}{3}$
∴tan∠BFO=$\sqrt{3}$,
所以二面角B-AD-C的正切值为$\sqrt{3}$.
点评 本题主要考查空间点、线、面位置关系,二面角等基础知识,同时考查空间想象能力,推理论证能力和运算求解能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
集合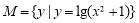 ,集合
,集合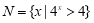 ,则
,则 等于( )
等于( )
A.[0,+∞) B.[0,1) C.(1,+∞) D.(0,1]
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
设函数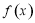 定义为如下数表,且对任意自然数
定义为如下数表,且对任意自然数 均有
均有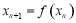 ,若
,若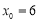 ,则
,则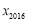 的值为( )
的值为( )
| 1 | 2 | 3 | 4 | 5 | 6 | …… |
| 5 | 1 | 3 | 2 | 6 | 4 | …… |
A.1 B.2 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
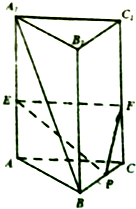 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB=2a,AE=CF=λAA1(0<λ<1),
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB=2a,AE=CF=λAA1(0<λ<1),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{e}$,2] | B. | [$\frac{5}{2e}$,2) | C. | (-$\frac{1}{2}$,-$\frac{5}{2e}$] | D. | [-2,-$\frac{5}{2e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com