
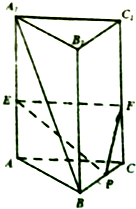
 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB=2a,AE=CF=λAA1(0<λ<1),
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB=2a,AE=CF=λAA1(0<λ<1),分析 (1)如图所示,连接A1C,交EF于点M,连接PM.由A1B∥面PEF,可得A1B∥MP.△A1BC中,可得$\frac{CP}{PB}$=$\frac{CM}{M{A}_{1}}$.利用AA1∥CC1,可得$\frac{CP}{PB}$=$\frac{λ}{1-λ}$,即可得出结论.
(2)在(1)的条件下,S△BPF=$\frac{1}{2}BP•CF$=(1-λ)λa2,由AE∥平面BCF,可得点E到平面BPF的距离即为AP=$\sqrt{3}$a,利用VE-BPF=$\frac{1}{3}×AP×{S}_{△BPF}$及其基本不等式的性质即可得出.
(3)在(2)的条件下,$λ=\frac{1}{2}$,即点P为线段BC的中点,点E,F分别为棱AA1,CC1的中点.取AB的中点Q,连接PQ,EQ,可得EF∥PQ.过点Q作QD⊥AC,作DG⊥EF,连接QG.可得∠DQG即为平面PEF与底面ABC所成的锐二面角.
解答 解:(1)如图所示,连接A1C,交EF于点M,连接PM.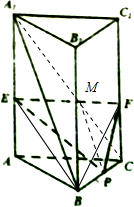
∵A1B∥面PEF,平面A1BC∩平面EFP=MP,∴A1B∥MP.
△A1BC中,$\frac{CP}{PB}$=$\frac{CM}{M{A}_{1}}$.
∵AA1∥CC1,∴$\frac{CM}{M{A}_{1}}$=$\frac{CF}{{A}_{1}E}$=$\frac{λC{C}_{1}}{(1-λ)A{A}_{1}}$=$\frac{λ}{1-λ}$.
∴$\frac{CP}{PB}$=$\frac{λ}{1-λ}$,即CP=λBC时,使得A1B∥面PEF.
(2)在(2)的条件下,S△BPF=$\frac{1}{2}BP•CF$=$\frac{1}{2}×$(1-λ)a×2λa=(1-λ)λa2,
∵AE∥平面BCF,∴点E到平面BPF的距离即为AP=$\sqrt{3}$a,
∴VE-BPF=$\frac{1}{3}×AP×{S}_{△BPF}$=$\frac{1}{3}×\sqrt{3}a$×(1-λ)λa2≤$\frac{\sqrt{3}{a}^{3}}{3}$×$(\frac{1-λ+λ}{2})^{2}$=$\frac{\sqrt{3}{a}^{3}}{12}$,当且仅当$λ=\frac{1}{2}$时取等号.
∴当λ=$\frac{1}{2}$时,四面体BPFE的体积最大为$\frac{\sqrt{3}{a}^{3}}{12}$.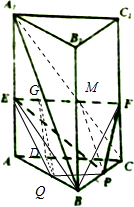
(3)在(2)的条件下,$λ=\frac{1}{2}$,即点P为线段BC的中点,点E,F分别为棱AA1,CC1的中点.
取AB的中点Q,连接PQ,EQ,则PQ∥AC,又EF∥AC,∴EF∥PQ.即PQ是平面PEF与底面ABC的交线.
过点Q作QD⊥AC,作DG⊥EF,垂足分别为D,G,连接QG.
则DQ⊥PQ,DG⊥底面ABC,∴QG⊥PQ,
∴∠DQG即为平面PEF与底面ABC所成的锐二面角.
在Rt△DQG中,tan∠DQG=$\frac{DG}{DQ}$=$\frac{a}{\frac{1}{2}×\frac{\sqrt{3}}{2}a}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查了空间位置关系空间角、等边三角形的性质、平行线分线段成比例定理、直角三角形的边角关系、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
在等差数列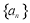 中,
中,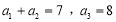 .令
.令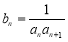 ,数列
,数列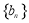 的前
的前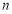 项和为
项和为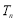 .
.
(1)求数列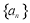 的通项公式;
的通项公式;
(2)求数列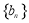 的前
的前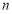 项和
项和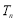 .
.
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
已知复数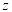 的共轭复数有
的共轭复数有 ,且满足
,且满足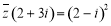 ,其中
,其中 是虚数单位,则复数
是虚数单位,则复数 的虚部为( )
的虚部为( )
A. B.
B.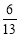 C.
C.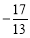 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
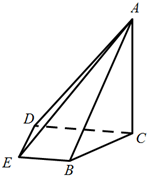 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
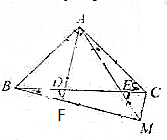 已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.
已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
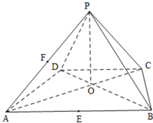 已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.
已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.
已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com