
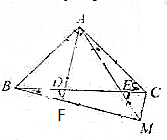
 已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.
已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.分析 (1)先求出∠B=45°,再证明∠DAE=∠B,即可证明:∠DAE=45°;
(2)证明A,C,M,B四点共圆,即可判断BM⊥CM.
解答 证明:(1)∵AB=AC,AB⊥AC,∴△ABC是等腰直角三角形,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠BAE=∠DAE+∠BAD,
∴∠ADC=∠BAE,
∴∠DAE=∠B=45°;
(2)∵BM⊥AF,∴∠AFM=90°.
∵∠FAM=∠DAE=45°,∴∠AMF=45°=∠ACB,
∴A,C,M,B四点共圆,
∴∠BAC+∠BMC=180°,
∵∠BAC=90°,
∴∠BMC=90°,即BM⊥CM.
点评 本题考查等腰直角三角形,考查四点共圆,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
设函数f(x)=logax(a>0,且a≠1),若f(x1x2…x2 017)=8,则f(x)+f(x)+…+f(x)的值等于( )
A.4 B.8 C.16 D.2loga8
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
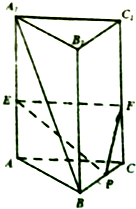 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB=2a,AE=CF=λAA1(0<λ<1),
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB=2a,AE=CF=λAA1(0<λ<1),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
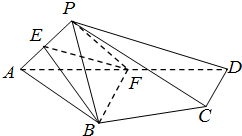 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com