
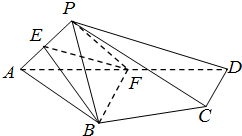
 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.分析 (I)连接BD,则△ABD为正三角形,于是BF⊥AD,根据面面垂直的性质得出BF⊥平面PAD,于是平面BEF⊥平面PAD;
(II)以F为原点建立空间直角坐标系,求出平面BEF和平面APB的法向量$\overrightarrow{m},\overrightarrow{n}$,求出二面角P-BE-F的余弦值再求出正切值.
解答 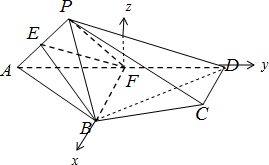 解:(I)证明:连接BD,
解:(I)证明:连接BD,
∵AB=AD,∠BAD=60°,∴△ABD是正三角形.
∵F是AD的中点,∴BF⊥AD.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
BF?平面ABCD,
∴BF⊥平面PAD,又BF?平面BEF,
∴平面BEF⊥平面PAD.
(II)在平面PAD内作AD的垂线FM,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,FM?平面PAD,
∴FM⊥平面ABCD,
以F为原点,以FB,FD,FM为坐标轴建立空间直角坐标系如图所示:
设AP=2,则F(0,0,0),B(4$\sqrt{3}$,0,0),A(0,-4,0),P(0,-3,$\sqrt{3}$),E(0,-$\frac{7}{2}$,$\frac{\sqrt{3}}{2}$).
∴$\overrightarrow{FE}$=(0,-$\frac{7}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{FB}$=(4$\sqrt{3}$,0,0),$\overrightarrow{AP}$=(0,1,$\sqrt{3}$),$\overrightarrow{AB}$=(4$\sqrt{3}$,4,0).
设平面BEF的法向量为$\overrightarrow{n}$=(x1,y1,z1),平面PBE的法向量为$\overrightarrow{m}$=(x2,y2,z2),
则$\left\{\begin{array}{l}{\overrightarrow{n}⊥\overrightarrow{FE}}\\{\overrightarrow{n}⊥\overrightarrow{FB}}\end{array}\right.$,$\left\{\begin{array}{l}{\overrightarrow{m}⊥\overrightarrow{AP}}\\{\overrightarrow{m}⊥\overrightarrow{AB}}\end{array}\right.$.
∴$\left\{\begin{array}{l}{-\frac{7}{2}{y}_{1}+\frac{\sqrt{3}}{2}{z}_{1}=0}\\{4\sqrt{3}{x}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{y}_{2}+\sqrt{3}{z}_{2}=0}\\{4\sqrt{3}{x}_{2}+4{y}_{2}=0}\end{array}\right.$.
令z1=1,得$\overrightarrow{n}$=(0,$\frac{\sqrt{3}}{7}$,1),令x2=1,得$\overrightarrow{m}$=(1,-$\sqrt{3}$,1).
∴$\overrightarrow{m}•\overrightarrow{n}$=-$\frac{3}{7}+1$=$\frac{4}{7}$,|$\overrightarrow{m}$|=$\sqrt{5}$,|$\overrightarrow{n}$|=$\frac{2\sqrt{13}}{7}$,
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\frac{4}{7}}{\sqrt{5}×\frac{2\sqrt{13}}{7}}$=$\frac{2\sqrt{65}}{65}$.
∴二面角P-BE-F的余弦值为$\frac{2\sqrt{65}}{65}$,
∴二面角P-BE-F的正切值为$\frac{\sqrt{61}}{2}$.
点评 本题考查了面面垂直的性质与判定,空间向量的应用与二面角的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:解答题
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.

(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
已知复数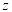 的共轭复数有
的共轭复数有 ,且满足
,且满足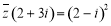 ,其中
,其中 是虚数单位,则复数
是虚数单位,则复数 的虚部为( )
的虚部为( )
A. B.
B.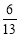 C.
C.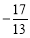 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
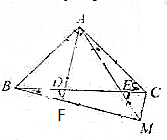 已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.
已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
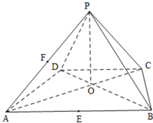 已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.
已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
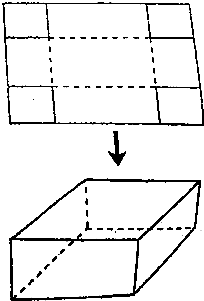 用长为16cm,宽为10cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四周的四个小矩形向上翻转90°角,再焊接而成(如图),问该容器的高x为多少时,容器的容积V(x)最大?最大容积是多少?
用长为16cm,宽为10cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四周的四个小矩形向上翻转90°角,再焊接而成(如图),问该容器的高x为多少时,容器的容积V(x)最大?最大容积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x+$\frac{1}{2}$ | B. | f(x)=-x2+x-$\frac{1}{4}$ | C. | f(x)=1-10x | D. | f(x)=ln(8x-7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com