
���� ��1����$Q��{\frac{4}{3}��\frac{b}{3}}��$ ������Բ���̿ɵã�$\frac{16}{9{a}^{2}}$+$\frac{{b}^{2}}{9{b}^{2}}$=1�����a2����P��0��b����F��c��0����$\overrightarrow{FP}$��$\overrightarrow{FQ}$���ɵ�$\overrightarrow{FP}$•$\overrightarrow{FQ}$=0����a2=b2+c2=2���������b��c���ɵó���ԲC�ķ��̣�
��2����ֱ��x=2�ϴ���һ��D��ʹ�á�ABDΪ�ȱ������Σ���ֱ��l�ķ���Ϊ��y=k��x-1����������Բ���̿ɵã���2k2+1��x2-4k2x+2k2-2=0�����ø���ϵ���Ĺ�ϵ���е����깫ʽ���ҳ���ʽ��ȱ������ε����ʼ��ɵó���
��� �⣺��1����$Q��{\frac{4}{3}��\frac{b}{3}}��$ ������Բ���̿ɵã�$\frac{16}{9{a}^{2}}$+$\frac{{b}^{2}}{9{b}^{2}}$=1�����a2=2��
��P��0��b����F��c��0����$\overrightarrow{FP}$=��c��-b����$\overrightarrow{FQ}$=$��\frac{4}{3}-c��\frac{b}{3}��$��
��$\overrightarrow{FP}$��$\overrightarrow{FQ}$����$\overrightarrow{FP}$•$\overrightarrow{FQ}$=$\frac{4}{3}c-{c}^{2}$-$\frac{{b}^{2}}{3}$=0��
��a2=b2+c2=2�����b=c=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{2}$+y2=1��
��2����ֱ��x=2�ϴ���һ��D��ʹ�á�ABDΪ�ȱ������Σ�
��ֱ��l�ķ���Ϊ��y=k��x-1����
������Բ���̿ɵã���2k2+1��x2-4k2x+2k2-2=0������0��
��A��x1��y1����B��x2��y2������x1+x2=$\frac{4{k}^{2}}{2{k}^{2}+1}$��x1•x2=$\frac{2{k}^{2}-2}{2{k}^{2}+1}$��
��AB���е�ΪM��x0��y0������x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{2{k}^{2}}{2{k}^{2}+1}$��y0=k��x0-1��=-$\frac{k}{2{k}^{2}+1}$��
|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}��{k}^{2}+1��}{2{k}^{2}+1}$��
�ߡ�DABΪ�ȱ������Σ���|DM|=$\frac{\sqrt{3}}{2}$|AB|��
��$\sqrt{\frac{1+{k}^{2}}{{k}^{2}}}$$•\frac{2{k}^{2}+2}{2{k}^{2}+1}$=$\frac{\sqrt{3}}{2}$•$\frac{2\sqrt{2}��{k}^{2}+1��}{2{k}^{2}+1}$�����k2=2����k=$��\sqrt{2}$��
����ֱ��x=2�ϴ���һ��D��ʹ�á�ABDΪ�ȱ������Σ�
��ʱֱ��l��б��Ϊ$��\sqrt{2}$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ����ת��ΪһԪ���η��̵ĸ���ϵ���Ĺ�ϵ���е����깫ʽ���ҳ���ʽ���ȱ������ε����ʡ�������ֱ���������Ĺ�ϵ��Բ�����ʣ���������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
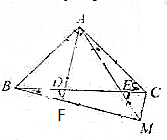 ��֪���ڡ�ABC�У�AB=AC��AB��AC��D��E��BC�ϣ��ҡ�ADC=��BAE��
��֪���ڡ�ABC�У�AB=AC��AB��AC��D��E��BC�ϣ��ҡ�ADC=��BAE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=2x+$\frac{1}{2}$ | B�� | f��x��=-x2+x-$\frac{1}{4}$ | C�� | f��x��=1-10x | D�� | f��x��=ln��8x-7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��R��Բ��ΪQ��Բ��x+$\sqrt{3}$��2+y2=16�ϵ�һ�����㣬N��$\sqrt{3}$��0��Ϊ���㣬�߶�RN���д�����ֱ��QR���ڵ�T����T��Ĺ켣Ϊ����C��
��֪��R��Բ��ΪQ��Բ��x+$\sqrt{3}$��2+y2=16�ϵ�һ�����㣬N��$\sqrt{3}$��0��Ϊ���㣬�߶�RN���д�����ֱ��QR���ڵ�T����T��Ĺ켣Ϊ����C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com