
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;
(Ⅱ)设g(x)=$\frac{4}{3}$sinx-$\frac{1}{6}$sin2x-x,设h(x)=$\frac{8}{3}$sinx-sin2x+$\frac{1}{12}$sin4x-x,根据函数的单调性证明即可;
(Ⅲ)(1)令x=$\frac{π}{3}$,代入$\frac{4}{3}$sinx-$\frac{1}{6}$sin2x<x<$\frac{8}{3}$sinx-sin2x+$\frac{1}{12}$sin4x中,整理即可;
(2)得到s6=$\frac{3\sqrt{3}}{2}$,s12=3,在$\frac{4}{3}$S2n一$\frac{1}{3}$Sn<π<$\frac{8}{3}$S2n一2Sn+$\frac{1}{3}{S_{\frac{n}{2}}}$中,令n=12,代入整理即可.
解答 解:(Ⅰ)f′(x)=-8sinx+12sin2x-4sin4x
=8sinx(-1+3cosx-2cosxcos2x)
=8sinx(1-cosx0(4cos2x+4cosx-1);
x∈(0,$\frac{π}{3}$)时,得sinx>0,1-cosx>0,
由cosx>$\frac{1}{2}$,得:4cos2x+4cosx-1>0,
古f′(x)>0,即f(x)在[0,$\frac{π}{3}$)递增,
又f(0)=3,故f(x)在[0,$\frac{π}{3}$)的最小值是3;
(Ⅱ)设g(x)=$\frac{4}{3}$sinx-$\frac{1}{6}$sin2x-x,
x∈(0,$\frac{π}{3}$)时,g′(x)=$\frac{4}{3}$cosx-$\frac{1}{3}$cos2x-1=-$\frac{2}{3}$(cosx-1)2<0,
故g(x)在[0,$\frac{π}{3}$)递减,得g(x)<g(0)=0,
即$\frac{4}{3}$sinx-$\frac{1}{6}$sin2x<x,①,
设函数h(x)=$\frac{8}{3}$sinx-sin2x+$\frac{1}{12}$sin4x-x,
h′(x)=$\frac{8}{3}$cosx-2cos2x+$\frac{1}{3}$cos4x-1=$\frac{1}{3}$f(x)-1,
x∈(0,$\frac{π}{3}$)时,由(Ⅰ)知f(x)>3,得h′(x)>0,
故h(x)在[0,$\frac{π}{3}$)上递增,
得h(x)>h(0)=0,即$\frac{8}{3}$sinx-sin2x+$\frac{1}{12}$sin4x>x,②,
综合①②,x∈(0,$\frac{π}{3}$)时,
有$\frac{4}{3}$sinx-$\frac{1}{6}$sin2x<x<$\frac{8}{3}$sinx-sin2x+$\frac{1}{12}$sin4x;
(Ⅲ)(1)令x=$\frac{π}{n}$,得:
$\frac{4}{3}$sin$\frac{π}{n}$-$\frac{1}{6}$sin$\frac{2π}{n}$<$\frac{π}{n}$<$\frac{8}{3}$sin$\frac{π}{n}$-sin$\frac{2π}{n}$+$\frac{1}{12}$sin$\frac{4π}{n}$,
即$\frac{4}{3}$sin$\frac{π}{n}$-$\frac{n}{6}$sin$\frac{2π}{n}$<π<$\frac{8}{3}$nsin$\frac{π}{n}$-nsin$\frac{2π}{n}$+$\frac{n}{12}$sin$\frac{4π}{n}$,
易知sn=$\frac{n}{2}$sin$\frac{2π}{n}$,s2n=nsin$\frac{π}{n}$,${s}_{\frac{n}{2}}$=$\frac{n}{4}$sin$\frac{4π}{n}$,
即$\frac{4}{3}$s2n-$\frac{1}{3}$sn<π<$\frac{8}{3}$S2n一2Sn+$\frac{1}{3}{S_{\frac{n}{2}}}$;
(2)易得,s6=$\frac{3\sqrt{3}}{2}$,s12=3,在$\frac{4}{3}$S2n一$\frac{1}{3}$Sn<π<$\frac{8}{3}$S2n一2Sn+$\frac{1}{3}{S_{\frac{n}{2}}}$中,令n=12,
得:π>$\frac{4}{3}$s24-$\frac{1}{3}$s12>$\frac{4}{3}$×3.105-$\frac{1}{3}$×3=3.14,
π<$\frac{8}{3}$s24-2s12+$\frac{1}{3}$s6<$\frac{8}{3}$×3.106-2×3+$\frac{1}{3}$×$\frac{3}{2}$×1.733<3.15,
综上,3.14<π<3.15.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,考查转化思想,是一道综合题.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
0<x<2是不等式|x+1|<3成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
设等差数列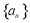 的前
的前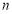 项和为
项和为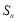 ,且满足
,且满足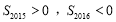 ,则前
,则前 项和
项和 取最大值时
取最大值时 的值为( )
的值为( )
A.1009 B.1008 C.1007 D.1006
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
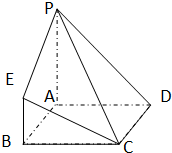 在四棱锥P-ABCD中,底面ABCD是边长为3的正方形,且 PA⊥面ABCD,PA∥BE,PA=3BE.
在四棱锥P-ABCD中,底面ABCD是边长为3的正方形,且 PA⊥面ABCD,PA∥BE,PA=3BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
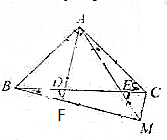 已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.
已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
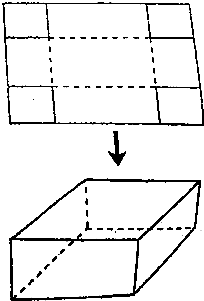 用长为16cm,宽为10cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四周的四个小矩形向上翻转90°角,再焊接而成(如图),问该容器的高x为多少时,容器的容积V(x)最大?最大容积是多少?
用长为16cm,宽为10cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四周的四个小矩形向上翻转90°角,再焊接而成(如图),问该容器的高x为多少时,容器的容积V(x)最大?最大容积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com