
分析 由题意设出M、N的坐标,联立直线与圆的方程,利用根与系数的关系得到M、N的横纵坐标的积,代入数量积的坐标运算得答案.
解答 解:设M(x1,y1),N(x2,y2),
联立$\left\{\begin{array}{l}{3x+4y+5=0}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,得25x2+30x-39=0.
则${x}_{1}+{x}_{2}=-\frac{30}{25},{x}_{1}{x}_{2}=-\frac{39}{25}$,
${y}_{1}{y}_{2}=\frac{15}{16}({x}_{1}+{x}_{2})+\frac{9}{16}{x}_{1}{x}_{2}+\frac{25}{16}$=$\frac{15}{16}×(-\frac{30}{25})+\frac{9}{16}×(-\frac{39}{25})+\frac{25}{16}$=$\frac{11}{25}$.
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$=${x}_{1}{x}_{2}+{y}_{1}{y}_{2}=-\frac{39}{25}+\frac{11}{25}=-\frac{28}{25}$
故答案为:$-\frac{28}{25}$.
点评 本题考查直线与圆的位置关系,考查了平面向量的数量积运算,是基础的计算题.


科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
已知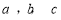 分别是
分别是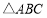 的内角
的内角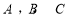 所对的边长,且
所对的边长,且 ,满
,满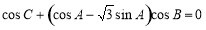 .
.
(1)求角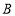 的大小;
的大小;
(2)若点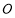 是
是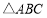 外一点,
外一点,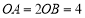 ,记
,记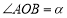 ,用含
,用含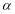 的三角函数式表示平面四边形
的三角函数式表示平面四边形 面积并求面积的最大值.
面积并求面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4和0 | B. | 4和1 | C. | $-\frac{4}{5}$和$\frac{8}{5}$ | D. | $\frac{8}{5}$和$-\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {x|x≤0,或x>1} | C. | {x|0≤x<1} | D. | (-∞,1)∪(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com