

| A. | 4和0 | B. | 4和1 | C. | $-\frac{4}{5}$和$\frac{8}{5}$ | D. | $\frac{8}{5}$和$-\frac{4}{5}$ |
分析 作出图形,取单位向量$\overrightarrow{i},\overrightarrow{j}$,从而可用$\overrightarrow{i},\overrightarrow{j}$分别表示出向量$\overrightarrow{a},\overrightarrow{b}$,再由$\overrightarrow{c}$=x$\overrightarrow a$+y$\overrightarrow b$,根据平面向量基本定理即可建立关于x,y的二元一次方程组,解出x,y,从而得出x+y的值.
解答 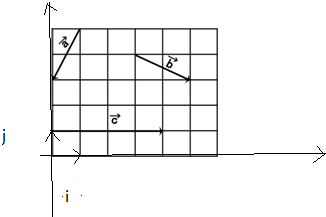 解:如图,取单位向量$\overrightarrow{i},\overrightarrow{j}$,则:$\overrightarrow{a}=-\overrightarrow{i}-2\overrightarrow{j}$,$\overrightarrow{b}=2\overrightarrow{i}-\overrightarrow{j}$,$\overrightarrow{c}=4\overrightarrow{i}$,
解:如图,取单位向量$\overrightarrow{i},\overrightarrow{j}$,则:$\overrightarrow{a}=-\overrightarrow{i}-2\overrightarrow{j}$,$\overrightarrow{b}=2\overrightarrow{i}-\overrightarrow{j}$,$\overrightarrow{c}=4\overrightarrow{i}$,
又$\overrightarrow c$=x$\overrightarrow a$+y$\overrightarrow b$,
∴4$\overrightarrow{i}$=x($-\overrightarrow{i}-2\overrightarrow{j}$)+y(2$\overrightarrow{i}-\overrightarrow{j}$)=(-x+2y)$\overrightarrow{i}$+(-2x-y)$\overrightarrow{j}$,
∴$\left\{\begin{array}{l}{-x+2y=4}\\{-2x-y=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=\frac{8}{5}}\end{array}\right.$,
故选:C.
点评 考查向量加法和数乘的几何意义,向量的数乘运算,以及平面向量基本定理.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{2}$+2 | C. | 4$\sqrt{2}$-2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com