
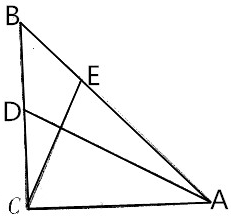
 如图,在等腰直角三角形ABC中,AC=BC,D是BC的中点,E是线段AB上的点,且AE=2BE.求证:AD⊥CE.
如图,在等腰直角三角形ABC中,AC=BC,D是BC的中点,E是线段AB上的点,且AE=2BE.求证:AD⊥CE. 分析 过B作BC的垂线交CE的延长线于点F,从而可推出AC∥BF,根据平行线的性质可得到两组对应角相等从而可判定△ACE∽△BFE,根据相似三角形的对应边对应成比例可得到AC=2BF,进而得到CD=BF,再利用HL判定△ACD≌△CBF,由全等三角形的性质得其对应角相等,再根据等角的性质不难证得结论.
解答  证明:过B作BC的垂线交CE的延长线于点F,(1分)
证明:过B作BC的垂线交CE的延长线于点F,(1分)
∴∠FBC=90°,
∵∠ACB=90°,
∴∠FBC=∠ACB=90°.
∴AC∥BF,
∴∠ACE=∠EFB,∠CAE=∠EBF
∴△ACE∽△BFE.(3分)
∴$\frac{AC}{BF}=\frac{AE}{EB}$=2.
∴AC=2BF.(4分)
∵D是BC的中点,∴BC=2CD,
∵AC=BC,
∴CD=BF.(5分)
在△ACD和△CBF中
$\left\{\begin{array}{l}{AC=CB}\\{∠ACB=∠CBF=90°}\\{CD=BF}\end{array}\right.$,
∴△ACD≌△CBF.(6分)
∴∠1=∠2.
∴∠2+∠3=∠1+∠3=90°.
∴∠4=90°.
∴CE⊥AD.(7分)
点评 此题主要考查学生对全等三角形的判定及性质及相似三角形的判定及性质的综合运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
已知x=ln π,y=log52,z= 则( )
则( )
A.x<y<z B.z<x<y C.z<y<x D.y<z<x
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
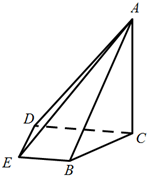 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,$AC=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
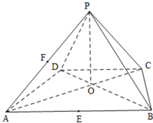 已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.
已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
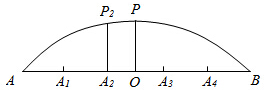 如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m
如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com