
分析 (1)求出函数的导数,得到f′(1)=2a-1+3=0,求出a的值,从而求出函数的单调区间即可;
(2)问题转化为若仅存在一个整数x0,使得f(x0)>k(x0+1)>0成立,令g(x)=k(x+1),则直线g(x)恒过(-1,0),得到$\left\{\begin{array}{l}{f(1)>g(1)}\\{f(2)<g(2)}\end{array}\right.$,解出即可.
解答 解:(1)f(x)=ax2-x+3lnx,x>0,
f′(x)=2ax-1+$\frac{3}{x}$,
若x=1是函数f(x)的一个极值点,
则f′(1)=2a-1+3=0,解得:a=-1,
∴f(x)=3lnx-x2-x,
f′(x)=$\frac{3}{x}$-2x-1=$\frac{-{2x}^{2}-x+3}{x}$=-$\frac{(2x+3)(x-1)}{x}$,
令f′(x)<0,解得:x>1,令f′(x)>0,解得:0<x<1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(2)若仅存在一个整数x0,使得f(x0)-kx0-k>0成立,
即若仅存在一个整数x0,使得f(x0)>k(x0+1)>0成立,
令g(x)=k(x+1),则直线g(x)恒过(-1,0),
由题意得:$\left\{\begin{array}{l}{f(1)>g(1)}\\{f(2)<g(2)}\end{array}\right.$即$\left\{\begin{array}{l}{-2>k(1+1)}\\{3ln2-4-2<k(2+1)}\end{array}\right.$,
解得:-2+ln2<k<-1.
点评 本题考查了切线方程问题,考查函数的单调性,考查导数的应用以及转化思想,是一道中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),且在区间[0,2]上是增函数,则( )
A.f(-25)<f(10)<f(80) B.f(80)<f(10)<f(-25)
C.f(10)<f(80)<f(-25) D.f(-25)<f(80)<f(10)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
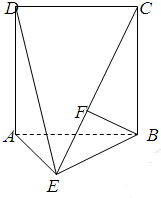 如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,F为CE上的点,且BF⊥平面ACE.
如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,F为CE上的点,且BF⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
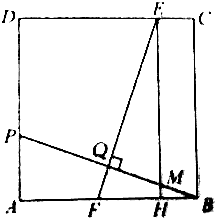 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD,AB于E,F两点.垂足为Q,过点E作EH⊥AB于点H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD,AB于E,F两点.垂足为Q,过点E作EH⊥AB于点H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com