
分析 (1)化圆的一般方程为标准方程,求出圆心坐标和半径,画出图形,再由椭圆的定义求得椭圆方程;
(2)假设椭圆上存在关于点N(2,-1)对称的两点G、H,则两点连线的斜率存在,设为k(k≠0),则GH:y=k(x-2)-1,联立直线方程和椭圆方程,利用根与系数的关系得到G、H两点横坐标的和,结合中点坐标公式列式求得k值,进一步求得两对称点的坐标.
解答 解:(1)如图,圆C:x2+y2+4x-28=0化为(x+2)2+y2=32,
圆心C(-2,0),半径r=$4\sqrt{2}$,点A(2,0),
∵P为MA的垂直平分线上的点,∴|PM|=|PA|,
则|PC|+|PA|=|CM|=r=$4\sqrt{2}$,
由椭圆定义可得,点P的轨迹是以C、A为焦点,以$4\sqrt{2}$为长轴长的椭圆,
且c=2,a=$2\sqrt{2}$,∴b2=a2-c2=8-4=4,
则点P的轨迹方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)∵$\frac{{2}^{2}}{8}+\frac{(-1)^{2}}{4}=\frac{3}{4}<1$,∴点N(2,-1)在椭圆$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$的内部,
假设椭圆上存在关于点N(2,-1)对称的两点G、H,则两点连线的斜率存在,设为k(k≠0),
则GH:y=k(x-2)-1,
联立$\left\{\begin{array}{l}{y=k(x-2)-1}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(1+2k2)x2-(8k2+4k)x+8k2+8k-6=0.①
则$\frac{8{k}^{2}+4k}{1+2{k}^{2}}=4$,解得k=1,代入①得:3x2-12x+10=0.
解得${x}_{1}=\frac{6-\sqrt{6}}{3},{x}_{2}=\frac{6+\sqrt{6}}{3}$.
代入y=x-3,得${y}_{1}=\frac{-3-\sqrt{6}}{3},{y}_{2}=\frac{-3+\sqrt{6}}{3}$.
∴点P的轨迹上存在关于点N(2,-1)对称的两点,
坐标分别为($\frac{6-\sqrt{6}}{3},\frac{-3-\sqrt{6}}{3}$),($\frac{6+\sqrt{6}}{3},\frac{-3+\sqrt{6}}{3}$).
点评 本题考查椭圆方程的求法,考查了直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
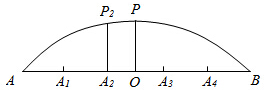 如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m
如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m查看答案和解析>>
科目:高中数学 来源: 题型:选择题
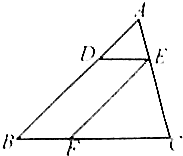 如图所示,已知D是△ABC中AB边上一点,DE∥BC且交AC于E,EF∥AB且交BC于F,且S△ADE=1,S△EFC=4,则四边形BFED的面积等于( )
如图所示,已知D是△ABC中AB边上一点,DE∥BC且交AC于E,EF∥AB且交BC于F,且S△ADE=1,S△EFC=4,则四边形BFED的面积等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com