
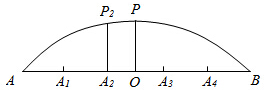
 如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m
如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m分析 以O为原点,AB方向为x轴正方向建立坐标系,则圆心在y轴,设圆心坐标,可得圆拱所在圆的方程,将x=-2代入圆方程,可求支柱A2P2的高度.
解答 解:以O为原点,AB方向为x轴正方向建立坐标系,则圆心在y轴,
设圆心坐标(0,a),P(0,4),A(-10,0)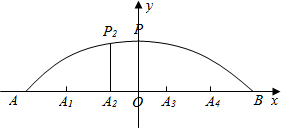 ,
,
则圆拱所在圆的方程为x2+(y-a)2=r2,
∴$\left\{\begin{array}{l}{(4-a)^{2}={r}^{2}}\\{(-10)^{2}+{a}^{2}={r}^{2}}\end{array}\right.$,
即(a-4)2=a2+100,解得a=-10.5,
∴圆方程为x2+(y+10.5)2=14.52 .
将x=-2代入圆方程,得:y=A2P2≈3.86(m).
故答案为:3.86m.
点评 本题考查圆的方程,考查学生的计算能力,确定圆心坐标是关键,是中档题.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
集合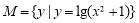 ,集合
,集合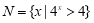 ,则
,则 等于( )
等于( )
A.[0,+∞) B.[0,1) C.(1,+∞) D.(0,1]
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{e}$,2] | B. | [$\frac{5}{2e}$,2) | C. | (-$\frac{1}{2}$,-$\frac{5}{2e}$] | D. | [-2,-$\frac{5}{2e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com