
分析 设MN=2MA,利用代入法求出N的轨迹方程,可得ON|min=$\sqrt{{8}^{2}+{2}^{2}}-2\sqrt{2}=2\sqrt{17}-2\sqrt{2}$,利用MO+2MA=MO+MN=ON,即可求出MO+2MA的最小值.
解答 解:如图,
设MN=2MA,N(x,y),M(a,b),则a=12-x,b=2-y,
代入圆C:(x-4)2+(y-4)2=8可得(12-x-4)2+(2-y-4)2=8,
即N的轨迹方程是(x-8)2+(y+2)2=8,
∴|ON|min=$\sqrt{{8}^{2}+{2}^{2}}-2\sqrt{2}=2\sqrt{17}-2\sqrt{2}$,
∵MO+2MA=MO+MN=ON,
∴MO+2MA的最小值为$2\sqrt{17}-2\sqrt{2}$,
故答案为:$2\sqrt{17}-2\sqrt{2}$.
点评 本题考查直线与圆的位置关系,考查代入法求轨迹方程,考查学生的计算能力,正确转化是关键,是中档题.


科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
在等差数列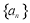 中,
中,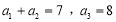 .令
.令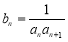 ,数列
,数列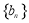 的前
的前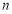 项和为
项和为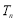 .
.
(1)求数列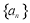 的通项公式;
的通项公式;
(2)求数列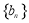 的前
的前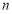 项和
项和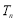 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
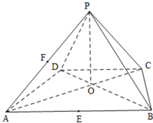 已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.
已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,$AB=2\sqrt{2},CD=\sqrt{2}$,E,F分别是AB,AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
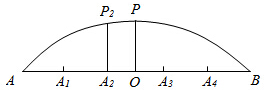 如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m
如图是某圆拱形桥一孔圆拱的示意图.这个图的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,则支柱A2P2=3.86m查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x+$\frac{1}{2}$ | B. | f(x)=-x2+x-$\frac{1}{4}$ | C. | f(x)=1-10x | D. | f(x)=ln(8x-7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.
已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com