
分析 (1)对x讨论,当x≥2时,当1<x<2时,当x≤1时,去掉绝对值,解不等式,最后求并集,即可得到所求解集;
(2)运用绝对值不等式的性质可得f(x)的最小值1,假设存在正数a、b,同时满足:2a+b=1,$\frac{1}{a}$+$\frac{2}{b}$=4.消去b,解关于a的方程,即可得到结论.
解答 解:(1)f(x)≤x+1,即为:
|x-1|+|x-2|≤x+1,
当x≥2时,x-1+x-2≤x+1,即x≤4,可得2≤x≤4;
当1<x<2时,x-1+2-x≤x+1,即x≥0,可得1<x<2;
当x≤1时,1-x+2-x≤x+1,即x≥$\frac{2}{3}$,可得$\frac{2}{3}$≤x≤1.
综上可得,原不等式的解集为[$\frac{2}{3}$,4];
(2)不存在正数a、b,同时满足:2a+b=1,$\frac{1}{a}$+$\frac{2}{b}$=4.
理由如下:函数f(x)=|x-1|+|x-2|≥|(x-1)-(x-2)|=1,
当且仅当(x-1)(x-2)≤0,即1≤x≤2时,f(x)取得最小值1,
假设存在正数a、b,同时满足:2a+b=1,$\frac{1}{a}$+$\frac{2}{b}$=4.
将b=1-2a代入第二式,可得$\frac{1}{a}$+$\frac{2}{1-2a}$=4,
即为8a2-4a+1=0,
由判别式为16-4×8×1=-16<0,
可得方程无实数解.
则不存在正数a、b,同时满足:2a+b=1,$\frac{1}{a}$+$\frac{2}{b}$=4.
点评 本题考查绝对值不等式的解法和存在性问题的解法,注意运用分类讨论的思想方法和假设存在,推理论证得出矛盾,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
设函数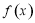 定义为如下数表,且对任意自然数
定义为如下数表,且对任意自然数 均有
均有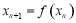 ,若
,若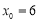 ,则
,则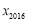 的值为( )
的值为( )
| 1 | 2 | 3 | 4 | 5 | 6 | …… |
| 5 | 1 | 3 | 2 | 6 | 4 | …… |
A.1 B.2 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{e}$,2] | B. | [$\frac{5}{2e}$,2) | C. | (-$\frac{1}{2}$,-$\frac{5}{2e}$] | D. | [-2,-$\frac{5}{2e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
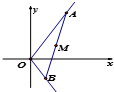 如图,点A,B分别在射线l1:y=2x(x≥0),l2:y=-2x(x≥0)上运动,且S△AOB=4.
如图,点A,B分别在射线l1:y=2x(x≥0),l2:y=-2x(x≥0)上运动,且S△AOB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com