
���� ����ͨ���ڲ���ʽan+1=2an+1����ͬʱ����1�ɹ���������Ⱦ�Ϊ2�ĵȱ�����{an+1}����������ɵý��ۣ�
����ͨ��A=1��B=1��C=0�ɵ�an��1����i����an+1=an+$\frac{1}{{a}_{n}}$����ͬʱƽ�������an��1�ɵý��ۣ���ii��ͨ��������֪���⼴֤2n-1��an2��3n-2����ϣ�i�����ۣ������ۼӷ����㼴�ý��ۣ�
��� ���⣺��A=2��B=0��C=1��
��an+1=2an+1��an+1+1=2��an+1����
�֡�a1+1=2��
������{an+1}��������Ⱦ�Ϊ2�ĵȱ����У�
��an=-1+2n��
����֤������A=1��B=1��C=0��
��an+1=an+$\frac{1}{{a}_{n}}$��
�֡�a1=1��
��an��1��
��i����an+1=an+$\frac{1}{{a}_{n}}$��
��${{a}_{n+1}}^{2}$=${{a}_{n}}^{2}$+2+$\frac{1}{{{a}_{n}}^{2}}$��
�֡�0��$\frac{1}{{{a}_{n}}^{2}}$��1��
��2��2+$\frac{1}{{{a}_{n}}^{2}}$��3����2��an+12-an2��3��
��ii��Ҫ֤��$\frac{3n-1}{3n-2}$��$\frac{{a}_{n+1}}{{a}_{n}}$��$\frac{2n}{2n-1}$��
��֤$\frac{1}{3n-2}$��$\frac{1}{{{a}_{n}}^{2}}$��$\frac{1}{2n-1}$��
��֤2n-1��an2��3n-2��
���ɣ�i����֪2��an2-an-12��3��2��an-12-an-22��3������2��a22-a12��3��
�ۼӵã�2��n-1����an2-a12��3��n-1����
��a1=1��֪2n-1��an2��3n-2���Ӷ������֤��
���� ������һ�����������벻��ʽ���ۺ��⣬������������ۼӷ��������������������ע����ⷽ���Ļ��ۣ������е��⣮


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�찲������һ�и�����ѧ���¿�����ѧ���ģ��Ծ��������棩 ���ͣ�ѡ����
��֪���� ������5����㣬��ʵ��
������5����㣬��ʵ��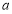 ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A��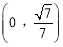 B��
B��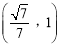 C.
C. D��
D��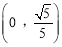
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
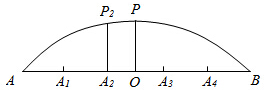 ��ͼ��ijԲ������һ��Բ����ʾ��ͼ�����ͼ��Բ�����AB=20m������OP=4m������ʱÿ���4m��Ҫ��һ��֧��֧�ţ���֧��A2P2=3.86m
��ͼ��ijԲ������һ��Բ����ʾ��ͼ�����ͼ��Բ�����AB=20m������OP=4m������ʱÿ���4m��Ҫ��һ��֧��֧�ţ���֧��A2P2=3.86m�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
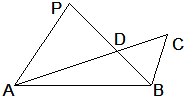 ��ͼ����֪PA=PB����APB=2��ACB��AC��PB���ڵ�D����PB=4��PD=3��AD=5����DC=$\frac{7}{5}$��
��ͼ����֪PA=PB����APB=2��ACB��AC��PB���ڵ�D����PB=4��PD=3��AD=5����DC=$\frac{7}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{4}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{��}{2}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com