
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 由题意画出图形,在△OPQ中,由正弦定理可得$sin∠OPQ=OQ•\frac{sin∠OQP}{OP}=2•\frac{sin∠OQP}{OP}$,知当∠OQP=90°,且OP最小时,sin∠OPQ有最大值,由点到直线的距离公式求出OP的最小值,则答案可求.
解答 解:如图,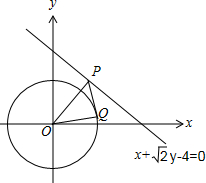
连接OP、OQ、PQ,
在△OPQ中,由正弦定理得:$\frac{OQ}{sin∠OPQ}=\frac{OP}{sin∠OQP}$,
∴$sin∠OPQ=OQ•\frac{sin∠OQP}{OP}=2•\frac{sin∠OQP}{OP}$,
∴当∠OQP=90°,且OP最小时,sin∠OPQ有最大值,
此时$O{P}_{min}=\frac{|-4|}{\sqrt{3}}=\frac{4}{\sqrt{3}}$,∴$(sin∠OPQ)_{max}=\frac{\sqrt{3}}{2}$,则∠OPQ的最大值为$\frac{π}{3}$.
故选:B.
点评 本题考查直线与圆的位置关系的应用,考查了数学转化思想方法,训练了正弦定理的应用,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
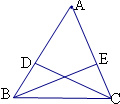
| A. | AE=AD | B. | ∠AEB=∠ADC | C. | CE=BD | D. | AB=AC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com