
分析 通过设P(m,n)(不妨令m、n均为正数),利用△APF为等腰三角形及直角三角形,求出n,m,通过抛物线的定义求解即可.
解答 解:由题可知:抛物线y2=8x的焦点为:F(2,0),
抛物线y2=8x的准线方程为:x=-2,
不妨设P(m,n)(m、n均为正数),则8m=n2,
∴|PA|=2+m,|FA|=$\sqrt{{4}^{2}+{n}^{2}}$,
由抛物线的定义可知:|PF|=|PA|=2+m,
∴△APF为等腰三角形,
又∠AFx=$\frac{2π}{3}$,∴2p=|FA|cos60°,|FA|=8.
即$\sqrt{{4}^{2}+{n}^{2}}$=8,n2=48.
得:8m=48,
解得:m=6,|PF|=2+6=8
故答案为:8.
点评 本题以抛物线为载体,考查求线段长度,考查抛物线的简单性质的应用,注意解题方法的积累,属于中档题.


科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
已知复数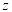 的共轭复数有
的共轭复数有 ,且满足
,且满足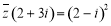 ,其中
,其中 是虚数单位,则复数
是虚数单位,则复数 的虚部为( )
的虚部为( )
A. B.
B.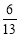 C.
C.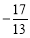 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x+$\frac{1}{2}$ | B. | f(x)=-x2+x-$\frac{1}{4}$ | C. | f(x)=1-10x | D. | f(x)=ln(8x-7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.
已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
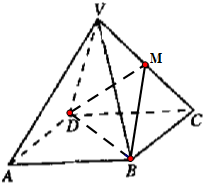 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形,M为VC边中点.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形,M为VC边中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com