
分析 (Ⅰ)利用椭圆的定义求出a,然后求解b,即可得到椭圆的方程.
(Ⅱ)设直线l的方程为y=kx+2(k≠0).M,N两点的坐标分别为(x1,y1),(x2,y2).联立方程:$\left\{\begin{array}{l}y=kx+2\\{x^2}+2{y^2}=4\end{array}\right.$,利用韦达定理通过$\overrightarrow{OM}⊥\overrightarrow{ON}$,所以x1x2+y1y2=0,求出,k即可推出结果.
解答 解:(Ⅰ)由题意可得2a=AC+BC
=$\sqrt{(\sqrt{2}-(-\sqrt{2}))^{2}+(1-0)^{2}}$+$\sqrt{(\sqrt{2}-\sqrt{2})^{2}+(1-0)^{2}}$
=4$>2\sqrt{2}$…(2分)
∴a=2∴b2=a2-c2=4-2=2.
∴椭圆的标准方程是$\frac{x^2}{4}+\frac{y^2}{2}=1$.…(4分)
(Ⅱ)由题意直线的斜率存在,可设直线l的方程为y=kx+2(k≠0).
设M,N两点的坐标分别为(x1,y1),(x2,y2).
联立方程:$\left\{\begin{array}{l}y=kx+2\\{x^2}+2{y^2}=4\end{array}\right.$…(5分)
消去y整理得,(1+2k2)x2+8kx+4=0
有${x_1}+{x_2}=-\frac{8k}{{1+2{k^2}}},{x_1}{x_2}=\frac{4}{{1+2{k^2}}}$…(7分)
若以MN为直径的圆恰好过原点,则$\overrightarrow{OM}⊥\overrightarrow{ON}$,所以x1x2+y1y2=0,…(8分)
所以,x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0…(9分)
所以,$\frac{{4({1+{k^2}})}}{{1+2{k^2}}}-\frac{{16{k^2}}}{{1+2{k^2}}}+4=0$
即$\frac{{8-4{k^2}}}{{1+2{k^2}}}=0$,…(10分)
得k2=2,k=$±\sqrt{2}$,
所以直线l的方程为$y=\sqrt{2}x+2$,或$y=-\sqrt{2}x+2$.
所以过P(0,2)的直线l:$y=±\sqrt{2}x+2$,使得以弦MN为直径的圆恰好过原点.…(12分)
点评 本题考查直线与椭圆位置关系的综合应用,椭圆方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
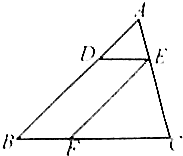 如图所示,已知D是△ABC中AB边上一点,DE∥BC且交AC于E,EF∥AB且交BC于F,且S△ADE=1,S△EFC=4,则四边形BFED的面积等于( )
如图所示,已知D是△ABC中AB边上一点,DE∥BC且交AC于E,EF∥AB且交BC于F,且S△ADE=1,S△EFC=4,则四边形BFED的面积等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com