
分析 (1)由题意可设抛物线的方程为:y2=2px(p>0),与直线x-y+1=0联立可得:x2+(2-2p)x+1=0,利用直线与抛物线相切的性质可得△=0,解得p即可得出.
(2)由△PAM与△PBM的面积之比等于$\frac{|PA|}{|PB|}$,可得直线x=1是∠AMB的平分线,因此直线PA与PB的斜率存在且kPA=-kPB.设A(x1,y1),B(x2,y2),利用斜率计算公式可得:kPA,kPB.由于点A,B在抛物线上,${y}_{1}^{2}$=4x1,${y}_{2}^{2}=4{x}_{2}$,代入化简可得:y1+y2=-4.又${y}_{1}^{2}$-${y}_{2}^{2}$=4(x1-x2),kl=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$,代入即可得出.
解答 解:(1)由题意可设抛物线的方程为:y2=2px(p>0),与直线x-y+1=0联立可得:x2+(2-2p)x+1=0,
∵直线x-y+1=0与C有唯一的公共点,∴△=(2-2p)2-4=0,
解得p=2.∴抛物线的方程为:y2=4x.
(2)∵△PAM与△PBM的面积之比等于$\frac{|PA|}{|PB|}$,
∴直线x=1是∠APB的平分线,∴直线PA与PB的斜率存在且kPA=-kPB.
设A(x1,y1),B(x2,y2),则kPA=$\frac{{y}_{1}-2}{{x}_{1}-1}$,
kPB=$\frac{{y}_{2}-2}{{x}_{2}-1}$,(x1,x2≠1).
由于点A,B在抛物线上,∴${y}_{1}^{2}$=4x1,${y}_{2}^{2}=4{x}_{2}$,
∴$\frac{{y}_{1}-2}{\frac{{y}_{1}^{2}}{4}-1}$=-$\frac{{y}_{2}-2}{\frac{{y}_{2}^{2}}{4}-1}$,化为:y1+y2=-4.
又${y}_{1}^{2}$-${y}_{2}^{2}$=4(x1-x2),∴kl=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{4}{{y}_{1}+{y}_{2}}$=-1.
∴l的斜率定值-1.
点评 本题考查了抛物线的标准方程及其性质、直线与相切问题问题转化为一元二次方程的判别式与0的关系、斜率计算公式、角平分线的性质,考查了推理能力与计算能力,属于难题.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
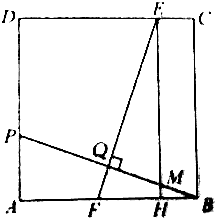 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD,AB于E,F两点.垂足为Q,过点E作EH⊥AB于点H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD,AB于E,F两点.垂足为Q,过点E作EH⊥AB于点H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
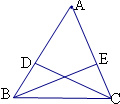
| A. | AE=AD | B. | ∠AEB=∠ADC | C. | CE=BD | D. | AB=AC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 7个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com