
分析 (Ⅰ)设P(x,y),则|x+1|=$\sqrt{(x-2)^{2}+{y}^{2}-3}$,由此能求出曲线E的方程.
(Ⅱ)设直线AB的方程为my=x-2,则直线CQ的方程为y=-m(x-2),将my=x-2代入y2=6x,得:y2-6my-12=0,由此利用韦达定理能求出存在常数λ使得|AC|•|BC|=λ|OC|2,并能求出λ的值,
解答 解:(Ⅰ)由已知得圆心为C(2,0),半径r=$\sqrt{3}$,
设P(x,y,),∵动点P到直线l:x=-1的距离等于
它到圆C:x2+y2-4x+1=0的切线长(P到切点的距离),
∴|x+1|=$\sqrt{(x-2)^{2}+{y}^{2}-3}$,整理,得y2=6x,
∴曲线E的方程为y2=6x.
(Ⅱ)设直线AB的方程为my=x-2,
则直线CQ的方程为y=-m(x-2),
解得Q(-1,3m),
∴|AC|•|BC|=(1+m2)|y1y2|=12(1+m2),|QC|2=9(1+m2),
∴|AC|•|BC|=$\frac{4}{3}$|QC|2.
∴λ=$\frac{4}{3}$.
点评 本题考查曲线方程的求法,考查满足条件的实数值是否存在的判断与求法,是中档题,解题时要认真审题,注意韦达定理、两点间距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
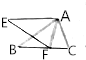 如图,已知△ABC≌△AEF,AB=BC,则下列结论中则下列结论正确的结论个数为( )
如图,已知△ABC≌△AEF,AB=BC,则下列结论中则下列结论正确的结论个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}-1}$与g(x)=$\sqrt{x-1}$•$\sqrt{x+1}$ | B. | f(x)=x与g(x)=$\frac{{x}^{3}+x}{{x}^{2}+1}$ | ||
| C. | y=x与y=($\sqrt{x}$)2 | D. | f(x)=$\sqrt{{x}^{2}}$与g(x)=$\root{3}{{x}^{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com