
分析 (1)设$\overrightarrow c=({λ,2λ})$,利用向量平行得到坐标的关系方程解之即可;
(2)利用向量垂直,数量积为0,得到$\overrightarrow a$与$\overrightarrow b$的数量积,再由数量积公式求夹角.
解答 解:(1)设∵$\overrightarrow c∥\overrightarrow a$,∴设$\overrightarrow c=({λ,2λ})$…(1分)
又∵$|{\overrightarrow c}|=2\sqrt{5}$,∴5λ2=20,即λ=±2…(2分)
$\overrightarrow c=({2,4})$或$\overrightarrow c=({-2,-4})$…(4分)
(2)$({\overrightarrow a+2\overrightarrow b})•({\overrightarrow a-\overrightarrow b})={\overrightarrow a^2}-2{\overrightarrow b^2}+\overrightarrow a•\overrightarrow b=0$…(5分)
∴$\overrightarrow a•\overrightarrow b=-\frac{5}{2}$…(6分)
∴$cosθ=\frac{\overrightarrow a•\overrightarrow b}{{|{\overrightarrow a}||{\overrightarrow b}|}}=\frac{{-\frac{5}{2}}}{{\sqrt{5}×\frac{{\sqrt{5}}}{2}}}=-1$…(7分)
∴θ=π…(8分)
点评 本题考查了平面向量平行和垂直的坐标运算,属于基础题.


科目:高中数学 来源: 题型:解答题
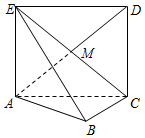 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | N?M | C. | M=N | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 接近0的实数可以构成集合 | |
| B. | R={实数集} | |
| C. | 集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合 | |
| D. | 参加2016年金砖国家峰会的所有国家可以构成一个集合 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com