
已知点Pn(an,bn)满足:对任意的n∈N,an+1=anbn+1,bn+1=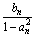 ,又知P0(
,又知P0(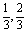 ).
).
(1)求过点P0、P1的直线l的方程;
(2)证明点Pn(n≥2)在直线l上;
(3)求点Pn的极限位置.
科目:高中数学 来源: 题型:
设f(x)=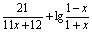 (-1<x<1).
(-1<x<1).
(1)求证:该函数在其定义域内是减函数.
(2)设h(x)=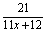 解方程f(x)-h(x)=-1.
解方程f(x)-h(x)=-1.
如果函数g(x)=lg(ax2+2f-1(0)x+1)的值域为全体实数,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义在R上的函数f(x)和数列{an}满足下列条件:
a1=a,an=f(aa-1)(n=2,3,4,…),a2≠a1,f(an)-f(an-1)=k(an-an-1)(n=2,3,4,…),其中a为常数,k为非零常
数.
(Ⅰ)令bn=aa+1-an(n∈N*),证明数列{bn}是等比数列;
(Ⅱ)求数列{an}的通项公式 ;
;
(Ⅲ)当|k|<1时,求
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等差数列{an}和等比数列{bn}各项都是正数,且a1=b1,a2n+1=b2n+1,那么一定有 ( )
A.an+1≤bn+1 B.an+1≥bn+1
C.an+1<bn+1 D.an+1>bn+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com