
科目:高中数学 来源: 题型:
用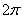 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为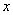 ,圆锥母线的长为
,圆锥母线的长为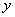
(1)、建立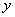 与
与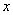 的函数关系式,并写出
的函数关系式,并写出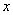 的取值范围;
的取值范围;
(2)、圆锥的母线与底面所成的角大小为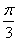 ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=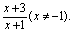 设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an-
设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an-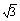 |,Sn=b1+b2+…+bn(n∈N*).
|,Sn=b1+b2+…+bn(n∈N*).
(Ⅰ)用数学归纳法证明bn≤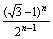 ;
;
(Ⅱ)证明Sn<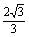 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点Pn(an,bn)满足:对任意的n∈N,an+1=anbn+1,bn+1=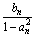 ,又知P0(
,又知P0(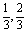 ).
).
(1)求过点P0、P1的直线l的方程;
(2)证明点Pn(n≥2)在直线l上;
(3)求点Pn的极限位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一条曲线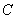 在
在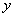 轴右侧,
轴右侧,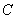 上每一点到点
上每一点到点 的距离减去它到
的距离减去它到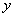 轴距离的差都是1。
轴距离的差都是1。
(1)求曲线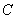 的方程;
的方程;
(2)设直线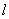 交曲线
交曲线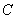 于
于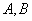 两点,线段
两点,线段 的中点为
的中点为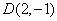 ,求直线
,求直线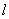 的一般式方程。
的一般式方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.(1)求椭圆C的标准方程;
(2)若直线l: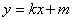 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证: 直线l过定点,并求出该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证: 直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
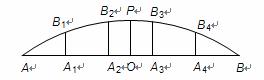
圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑。
(1)建立适当的坐标系,写出圆弧的方程;
(2)求支柱A2B2的高度(精确到0.01米)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com