
分析 (1)当n=1时,a1=2;当n≥2时,计算可得an=2an-1,所以数列{an}是首项为2,公比为2的等比数列,从而${a}_{n}={2}^{n}$;
(2)由(1)知log4an=$lo{g}_{4}{2}^{n}$=$\frac{n}{2}$,log4an+1=$lo{g}_{4}{2}^{n+1}$=$\frac{n+1}{2}$,所以bn=$\frac{1}{lo{g}_{4}{a}_{n}•lo{g}_{4}{a}_{n+1}}$=$\frac{1}{\frac{n}{2}•\frac{n+1}{2}}$=$4(\frac{1}{n}-\frac{1}{n+1})$,所以Tn=$4(1-\frac{1}{n+1})$;
(3)由(1)知不等式$\frac{2lo{g}_{4}{a}_{n}+2}{k}≤{n}^{2}$+4n+5等价于$\frac{n+2}{k}≤{n}^{2}+4n+5$,又k>0,可得kn2+(4k-1)n+5k-2≥0,由△≤0,解得$k≥\frac{1}{2}$.
解答 解:(1)当n=1时,a1=2a1-2,即a1=2,
当n≥2时,an=Sn-Sn-1=(2an-2)-(2an-1-2),
故an=2an-1,
所以数列{an}是首项为2,公比为2的等比数列,
则求{an}的通项公式为${a}_{n}={2}^{n}$;
(2)由(1)知log4an=$lo{g}_{4}{2}^{n}$=$\frac{n}{2}$,
log4an+1=$lo{g}_{4}{2}^{n+1}$=$\frac{n+1}{2}$,
所以bn=$\frac{1}{lo{g}_{4}{a}_{n}•lo{g}_{4}{a}_{n+1}}$
=$\frac{1}{\frac{n}{2}•\frac{n+1}{2}}$
=$\frac{4}{n(n+1)}$
=$4(\frac{1}{n}-\frac{1}{n+1})$,
则{bn}的前n项和为
Tn=$4(1-\frac{1}{2})$+$4(\frac{1}{2}-\frac{1}{3})$+…+$4(\frac{1}{n}-\frac{1}{n+1})$
=$4(1-\frac{1}{n+1})$;
(3)由(1)知log4an=$lo{g}_{4}{2}^{n}$=$\frac{n}{2}$,
所以$\frac{2lo{g}_{4}{a}_{n}+2}{k}$=$\frac{2×\frac{n}{2}+2}{k}$=$\frac{n+2}{k}$,
从而不等式$\frac{2lo{g}_{4}{a}_{n}+2}{k}≤{n}^{2}$+4n+5
等价于$\frac{n+2}{k}≤{n}^{2}+4n+5$,
又k>0,则上式整理
可得kn2+(4k-1)n+5k-2≥0,
则△=(4k-1)2-4k(5k-2)
=1-4k2≤0,
解得$k≥\frac{1}{2}$.
点评 本题考查求数列通项公式及前n项和的计算,运用裂项法求前n项和是关键,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,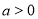 ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
.
(1)求曲线 的普通方程,并将
的普通方程,并将 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)直线 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 与
与 的公共点都在
的公共点都在 上,求
上,求 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$)∪[$\sqrt{2}$,+∞) | B. | [-2,2] | C. | [-2,-$\sqrt{2}$]∪[$\sqrt{2}$,2] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com