
分析 (1)设AB的方程为$\frac{x}{a}+\frac{y}{b}$=1(a>0,b>0),可得$\frac{1}{a}+\frac{2}{b}$=1,利用基本不等式算出ab≥8,可得当且仅当a=2且b=4时,△AOB的面积S有最小值为4,进而算出此时的直线l方程;
(2)求出|PA|,|PB|,利用二倍角的正弦公式算出|PA|•|PB|,由正弦函数的值域可得直线斜率为-1,利用点斜式方程列式,化简可得直线l的方程.
解答 解:(1)设直线AB的方程为$\frac{x}{a}+\frac{y}{b}$=1(a>0,b>0),
∵点P(1,2)在直线上,
∴$\frac{1}{a}+\frac{2}{b}$=1,
由基本不等式1=$\frac{1}{a}+\frac{2}{b}$≥2$\sqrt{\frac{2}{ab}}$,当且仅当a=2且b=4时,等号成立,
∴ab≥8,可得△AOB的面积S=$\frac{1}{2}$ab≥4,
因此△AOB的面积S的最小值为4,
此时的直线方程为$\frac{x}{2}+\frac{y}{4}$=1,即2x+y-4=0;
(2)设直线的倾斜角为θ,则|PA|=$\frac{2}{sin(π-θ)}$=$\frac{2}{sinθ}$,|PB|=$\frac{1}{cos(π-θ)}$=-$\frac{1}{cosθ}$,
∴|PA|•|PB|=-$\frac{4}{sin2θ}$
当2θ=$\frac{3}{2}$π,即θ=$\frac{3}{4}π$时,|PA|•|PB|取最小值4,
此时,直线的斜率为-1,
直线l的方程为y-2=-1(x-1),化为一般式可得x+y-3=0.
点评 本题给出直线经过定点,求满足特殊条件的直线方程,着重考查了直线的基本量与基本形式、三角形面积的计算和基本不等式求最值等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
 | 7 | 8 | 9 | 10 |
| 甲 | 0.2 | 0.15 | 0.3 | |
| 乙 | 0.2 | 0.2 | 0.35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
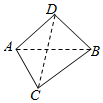 如图,已知三棱锥D-ABC的底面ABC为等边三角形,AB=CD=2,AD=BD=$\sqrt{2}$.
如图,已知三棱锥D-ABC的底面ABC为等边三角形,AB=CD=2,AD=BD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com