
【题目】已知函数![]() .
.
(1)求证:对任意实数![]() ,都有
,都有![]() ;
;
(2)若![]() ,是否存在整数
,是否存在整数![]() ,使得在
,使得在![]() 上,恒有
上,恒有![]() 成立?若存在,请求出
成立?若存在,请求出![]() 的最大值;若不存在,请说明理由.(
的最大值;若不存在,请说明理由.(![]() )
)
【答案】(1)见证明;(2)见解析
【解析】
(1)利用导数求得![]()
![]() ,令
,令![]() ,再利用导数即可求得
,再利用导数即可求得![]() ,问题得证。
,问题得证。
(2)整理![]() 得:
得:![]() ,令:
,令:![]() ,由
,由![]() 得
得![]() ,对
,对![]() 是否大于
是否大于![]() 分类, 当
分类, 当![]() 时,即
时,即![]() 时,利用导数即可证得
时,利用导数即可证得![]() ,当
,当![]() 时,利用导数即可求得
时,利用导数即可求得![]() ,要使不等式
,要使不等式![]() 恒成立转化成
恒成立转化成![]() 成立,令
成立,令![]() ,利用导数即可求得
,利用导数即可求得![]() ,
,![]() ,即可求得
,即可求得![]() ,问题得解。
,问题得解。
解:(1)证明:由已知易得![]() ,所以
,所以![]()
令![]() 得:
得:![]()
显然,![]() 时,
时,![]() <0,函数f(x)单调递减;
<0,函数f(x)单调递减;
![]() 时,
时,![]() >0,函数f(x)单调递增
>0,函数f(x)单调递增
所以![]()
![]()
令![]() ,则由
,则由![]() 得
得![]()
![]() 时,
时,![]() >0,函数t(
>0,函数t(![]() )单调递增;
)单调递增;
![]() 时,
时,![]() <0,函数t(
<0,函数t(![]() )单调递减
)单调递减
所以![]() ,即结论成立.
,即结论成立.
(2)由题设化简可得![]()
令![]() ,所以
,所以![]()
由![]() =0得
=0得![]()
①若![]() ,即
,即![]() 时,在
时,在![]() 上,有
上,有![]() ,故函数
,故函数![]() 单调递增
单调递增
所以![]()
②若![]() ,即
,即![]() 时,
时,
在![]() 上,有
上,有![]() ,故函数
,故函数![]() 在
在![]() 上单调递减
上单调递减
在![]() 上,有
上,有![]() .故函数
.故函数![]() 在
在![]() 上单调递增
上单调递增
所以,在![]() 上,
上,![]()
故欲使![]() ,只需
,只需![]() 即可
即可
令![]()
由![]() 得
得![]()
所以,![]() 时,
时,![]() ,即
,即![]() 单调递减
单调递减
又![]()
![]()
故![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ln(a x)+bx在点(1,f(1))处的切线是y=0;
(I)求函数f(x)的极值;
(II)当![]() 恒成立时,求实数m的取值范围(e为自然对数的底数)
恒成立时,求实数m的取值范围(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 为椭圆上一动点,当
为椭圆上一动点,当![]() 的面积最大时,其内切圆半径为
的面积最大时,其内切圆半径为![]() ,设过点
,设过点![]() 的直线
的直线![]() 被椭圆
被椭圆![]() 截得线段
截得线段![]() ,
,
当![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() 是椭圆上异于左、右顶点的两点,设直线
是椭圆上异于左、右顶点的两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否过定点?若过定点,求该定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 长轴的一个端点是抛物线
长轴的一个端点是抛物线![]() 的焦点,且椭圆焦点与抛物线焦点的距离是1。
的焦点,且椭圆焦点与抛物线焦点的距离是1。
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 的左右端点,
的左右端点,![]() 为原点,
为原点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别交
分别交![]() 轴于
轴于![]() ,问
,问![]() 是否为定值,说明理由。
是否为定值,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iphone手机的年固定成本为40万美元,每生产1万部还需要另外投入16美元,设苹果公司一年内共生产该款iphone手机![]() 万部并全部销售完,每万部的销售收入为
万部并全部销售完,每万部的销售收入为![]() 万元,且
万元,且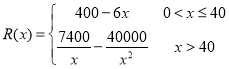 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万部)的函数解析式;
(万部)的函数解析式;
(2)当年产量为多少万部时,苹果公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的定义域
的定义域![]() 恰是不等式
恰是不等式![]() 的解集,其值域为
的解集,其值域为![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .
.
(1)求![]() 定义域
定义域![]() 和值域
和值域![]() ;
;
(2)试用单调性的定义法解决问题:若存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围并用
的取值范围并用![]() 表示
表示![]() ;
;
(3)是否存在实数![]() ,使
,使![]() 成立?若存在,求实数
成立?若存在,求实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com