
| �������� | [0��30�� | [30��60�� | [60��90�� | [90��120�� | [120��150] |
| �Ŀ�Ƶ�� | 2 | 4 | 8 | 3 | 3 |
| ����Ƶ�� | 3 | 7 | 12 | 20 | 8 |
| ���� ʧ�� | �� | �� |
| ���� | 15 | 30 |
| ���� | 5 | 20 |
| P��K2��k�� | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1������ƽ������ʽ����������Ŀ���ѧƽ���֣��ٸ��ݱ������ݿ�������ƿ����ļ���������
��2�����ö����Լ���Ĺ�ʽ�����K2=1.4��2.706�����ж�û��90%�İ�����Ϊ����ʧ�����ġ��������IJ�ͬ�йأ�
��� �⣺��1����$\frac{15��2+45��4+75��8+105��3+135��3}{20}=76.5$
������Ŀ���ѧƽ����Ϊ76.5������3�֣�
��$1400��\frac{50}{70}=1000$��$1000��\frac{20+8}{50}=560$��
�����ƿ�����560�˼�����6�֣�
��2��${k^2}=\frac{{70��{{��{15��20-5��30}��}^2}}}{20��50��25��45}=1.4��2.706$������10�֣�
��û��90%�İ�����Ϊ����ʧ�����ġ��������IJ�ͬ�йأ�����12�֣�
���� ���⿼��ƽ������Ƶ��������������Լ����Ӧ�ã����е��⣬����ʱҪ�������⣬ע�����ݴ���������������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��2\sqrt{2}��+�ޣ�$ | B�� | $[2\sqrt{2}��+�ޣ�$ | C�� | ��3��+�ޣ� | D�� | [3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
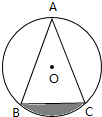 ��ͼ��������ABCΪ��O�ڽ������Σ��Ҷ��ǡ�A=30�㣬��O�뾶r=6cm����
��ͼ��������ABCΪ��O�ڽ������Σ��Ҷ��ǡ�A=30�㣬��O�뾶r=6cm�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {3} | B�� | {0��3} | C�� | {-1��4} | D�� | {0��3��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��1 | B�� | a��-1 | C�� | a��1��a��-1 | D�� | a��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com