
分析 (1)根据f(1)=1,f(2)=log212,代入函数的解析式得到关于a,b的方程组,解出即可;
(2)根据函数单调性的对于证明即可.
解答 解:(1)由$\left\{{\begin{array}{l}{f(1)={{log}_2}(a-b)=1}\\{f(2)={{log}_2}({a^2}-{b^2})={{log}_2}12}\end{array}}\right.$,得:$\left\{{\begin{array}{l}{a-b=2}\\{{a^2}-{b^2}=12}\end{array}}\right.$,
解得a=4,b=2;…(4分)
(2)由(1)得$f(x)={log_2}({4^x}-{2^x})$…(5分)
由4x-2x>0,得2x-1>0,解得:x>0…(6分)
∴f(x)的定义域为(0,+∞)…(7分)
设x1>x2>0,
则${4^{x_1}}-{2^{x_1}}-({4^{x_2}}-{2^{x_2}})=({4^{x_1}}-{4^{x_1}})-({2^{x_1}}-{2^{x_2}})$
=$({2^{x_1}}-{2^{x_2}})({2^{x_1}}+{2^{x_2}}-1)$…(9分)
∵x1>x2>0,∴${2^{x_1}}>{2^{x_2}}>1$,
∴$({2^{x_1}}-{2^{x_2}})({2^{x_1}}+{2^{x_2}}-1)>0$,
∴${4^{x_1}}-{2^{x_1}}>{4^{x_2}}-{2^{x_2}}$…(10分)
又y=log2x在(0,+∞)上递增;
∴${log_2}({4^{x_1}}-{2^{x_1}})>{log_2}({4^{x_2}}-{2^{x_2}})$,
即f(x1)>f(x2)…(11分)
∴f(x)在定义域(0,+∞)内递增…(12分)
点评 本题考查了对数函数的性质,考查根据定义证明函数的单调性问题,是一道基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150] |
| 文科频数 | 2 | 4 | 8 | 3 | 3 |
| 理科频数 | 3 | 7 | 12 | 20 | 8 |
| 文理 失分 | 文 | 理 |
| 概念 | 15 | 30 |
| 其它 | 5 | 20 |
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
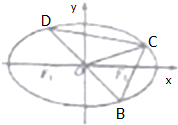 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的两焦点与短轴的一个端点的连线构成等边三角形,直线$x+y+2\sqrt{2}-1=0$与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的两焦点与短轴的一个端点的连线构成等边三角形,直线$x+y+2\sqrt{2}-1=0$与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 7816 6572 0802 6314 0214 4319 9714 0198 |
| 3204 9234 4936 8200 3623 4869 6938 7181 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com