
分析 由已知可得ax2+(b-2a)x+(c-b)≥0恒成立,即△=(b-2a)2-4a(c-b)=b2+4a2-4ac≤0,且a>0,进而利用基本不等式可得最大值.
解答 解:∵f′(x)=ax2+bx+c,
∴f′′(x)=2ax+b,
∵对任意x∈R,不等式f′(x)≥f′′(x)恒成立,
∴ax2+bx+c≥2ax+b恒成立,
即ax2+(b-2a)x+(c-b)≥0恒成立,
故△=(b-2a)2-4a(c-b)=b2+4a2-4ac≤0,且a>0,
即b2≤4ac-4a2,∴4ac-4a2≥0,∴c≥a>0,⇒$\frac{{b}^{2}}{{a}^{2}+2{c}^{2}}≤\frac{4ac-4{a}^{2}}{{a}^{2}+2{c}^{2}}=\frac{4(\frac{c}{a}-1)}{1+2(\frac{c}{a})^{2}}$=$\frac{4(\frac{c}{a}-1)}{2(\frac{c}{a}-1)^{2}+4(\frac{c}{a}-1)+3}$
∴当$\frac{c}{a}-1=0时,即a=c,b=0$,则$\frac{b^2}{{{a^2}+2{c^2}}}$=0,
$\frac{C}{a}-1>0$时,$\frac{b^2}{{{a^2}+2{c^2}}}$≤$\frac{4}{2(\frac{c}{a}-1)+\frac{3}{\frac{c}{a}-1}+4}≤\frac{4}{2\sqrt{\sqrt{6}}+4}$=$\sqrt{6}-2$,
故答案为$\sqrt{6}-2$
点评 本题考查了一元二次不等式恒成立问题,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{a}$,0) | B. | ($\frac{1}{2a}$,0) | ||
| C. | ($\frac{1}{4a}$,0) | D. | a>0 时为($\frac{1}{4a}$,0),a<0 时为(-$\frac{1}{4a}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
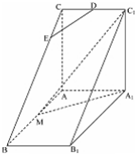 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,N是BC的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上的一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,N是BC的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2\sqrt{2},+∞)$ | B. | $[2\sqrt{2},+∞)$ | C. | (3,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com