
分析 根据已知中τ-函数,与Γ一函数的定义,逐一分析给定四个命题的真假,可得答案.
解答 解:当f(x)=ln(l+x)(x≠0)时,
满足对?x∈(-1,0)∪(0,+∞),都有f(x)<x,则(x)为τ-函数,即①正确;
当f(x)=sinx (0<x<π)时,
满足对?x∈(0,π)都有f[f(x)]<x,则f(x)为Γ一函数,即②正确.
f(x)为τ-函数时,对?x∈I,都有f(x)<x,
此时f(x)∈I不一定成立,故f[f(x)]<f(x)不一定成立,
故f(x)为τ-函数不是(x)为Γ一函数的充分条件,即③错误;
f(x)=ax2-1是τ一函数,即ax2-x-1<0恒成立,故a<-$\frac{1}{4}$,或a=0
f(x)=ax2-1是Γ一函数,即a(ax2-1)2-x-1<0恒成立,故a<-$\frac{1}{4}$,
即f(x)=ax2-1既是τ一函数又是Γ一函数的充要条件是a<-$\frac{1}{4}$.即④正确;
故答案为:①②④
点评 本题以命题的真假判断应用为载体,考查了全称命题,函数的图象和性质等知识点,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
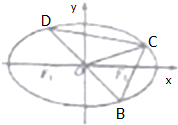 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的两焦点与短轴的一个端点的连线构成等边三角形,直线$x+y+2\sqrt{2}-1=0$与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的两焦点与短轴的一个端点的连线构成等边三角形,直线$x+y+2\sqrt{2}-1=0$与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com