
分析 根据等比数列的性质以及充分条件和必要条件的定义进行判断即可.
解答 解:∵{an}是首项为正数的等比数列,公比为q,
∴当a1=1,q=-$\frac{1}{2}$时,满足q<0,但此时a1+a2=1-$\frac{1}{2}$=$\frac{1}{2}$>0,则a2n-1+a2n<0不成立,即充分性不成立,
反之若a2n-1+a2n<0,则a1q2n-2+a1q2n-1<0
∵a1>0,∴q2n-2(1+q)<0,即1+q<0,
则q<-1,即q<0成立,即必要性成立,
则“q<0”是“对任意的正整数n,a2n-1+a2n<0”的必要不充分条件,
故答案为:必要不充分
点评 本题主要考查充分条件和必要条件的判断,根据等比数列的性质和公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
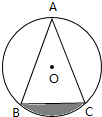 如图,等腰△ABC为⊙O内接三角形,且顶角∠A=30°,⊙O半径r=6cm,求:
如图,等腰△ABC为⊙O内接三角形,且顶角∠A=30°,⊙O半径r=6cm,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com