
【题目】下列命题中,假命题的个数是( )
(1)若直线a在平面![]() 上,直线b不在平面
上,直线b不在平面![]() 上,则a,b是异面直线;
上,则a,b是异面直线;
(2)若a,b是异面直线、则与a,b都垂直的直线有且只有一条
(3)若a,b是异面直线、若c,d与直线a,b都相交,则c,d也是异面直线
(4)设a,b是两条直线,若![]() 平面
平面![]() ,
,![]() ,则
,则![]() 平面
平面![]() .
.
A.1个B.2个C.3个D.4个
科目:高中数学 来源: 题型:
【题目】目前用外卖网点餐的人越来越多.现对大众等餐所需时间情况进行随机调查,并将所得数据绘制成频率分布直方图(如图).其中等餐所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
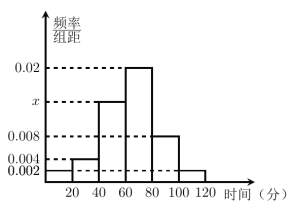
(1)求直方图中![]() 的值;
的值;
(2)某同学在某外卖网点了一份披萨,试估计他等餐时间不多于![]() 小时的概率;
小时的概率;
(3)现有![]() 名学生都分别通过外卖网进行了点餐,这
名学生都分别通过外卖网进行了点餐,这![]() 名学生中等餐所需时间少于
名学生中等餐所需时间少于![]() 小时的人数记为
小时的人数记为![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
|
| |
往返车费 | 3元 | 5元 |
服务老人的人数 | 5人 | 3人 |
根据安排,去敬老院的往返总车费不能超过37元,且![]() 小区参加献爱心活动的同学比
小区参加献爱心活动的同学比![]() 小区的同学至少多1人,则接受服务的老人最多有____人.
小区的同学至少多1人,则接受服务的老人最多有____人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,曲线![]() 由部分椭圆
由部分椭圆![]() :
:![]() 和部分抛物线
和部分抛物线![]() :
:![]() 连接而成,
连接而成,![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,其中
,其中![]() 所在椭圆的离心率为
所在椭圆的离心率为![]() .
.
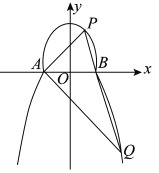
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() 中任意两点均不重合),若
中任意两点均不重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )

A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网约车的兴起丰富了民众出行的选择,为民众出行提供便利的同时也解决了很多劳动力的就业问题,据某著名网约车公司“滴滴打车”官网显示,截止目前,该公司已经累计解决退伍军人转业为兼职或专职司机三百多万人次,梁某即为此类网约车司机,据梁某自己统计某一天出车一次的总路程数可能的取值是20、22、24、26、28、![]() ,它们出现的概率依次是
,它们出现的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求这一天中梁某一次行驶路程X的分布列,并求X的均值和方差;
(2)网约车计费细则如下:起步价为5元,行驶路程不超过![]() 时,租车费为5元,若行驶路程超过
时,租车费为5元,若行驶路程超过![]() ,则按每超出
,则按每超出![]() (不足
(不足![]() 也按
也按![]() 计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com