
【题目】对于任意的![]() ,若数列
,若数列![]() 同时满足下列两个条件,则称数列
同时满足下列两个条件,则称数列![]() 具有“性质m”:
具有“性质m”:![]() ;
;![]() 存在实数M,使得
存在实数M,使得![]() 成立.
成立.
![]() 数列
数列![]() 、
、![]() 中,
中,![]() 、
、![]() (
(![]() ),判断
),判断![]() 、
、![]() 是否具有“性质m”;
是否具有“性质m”;
![]() 若各项为正数的等比数列
若各项为正数的等比数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,
,![]() ,求证:数列
,求证:数列![]() 具有“性质m”;
具有“性质m”;
![]() 数列
数列![]() 的通项公式
的通项公式![]() 对于任意
对于任意![]() ,数列
,数列![]() 具有“性质m”,且对满足条件的M的最小值
具有“性质m”,且对满足条件的M的最小值![]() ,求整数t的值.
,求整数t的值.
【答案】(1)数列![]() 不具有“m性质”; 数列
不具有“m性质”; 数列![]() 具有“性质m”(2)证明见解析;(3)
具有“性质m”(2)证明见解析;(3)![]()
【解析】
![]() 利用数列
利用数列![]() 具有“性质m”的条件对
具有“性质m”的条件对![]() 、
、![]() (
(![]() )判断即可;
)判断即可;![]() 数列
数列![]() 是各项为正数的等比数列,利用已知求得q,从而可求得
是各项为正数的等比数列,利用已知求得q,从而可求得![]() ,
,![]() 及
及![]() ,分析验证即可;
,分析验证即可;![]() 由于
由于![]() ,可求得
,可求得![]() ,
,![]() ,由
,由![]() 可求得
可求得![]() ,可判断
,可判断![]() 时,数列
时,数列![]() 是单调递增数列,且
是单调递增数列,且![]() ,从而可求得
,从而可求得![]() ,于是有
,于是有![]() ,经检验
,经检验![]() 不合题意,于是得到答案.
不合题意,于是得到答案.
![]() 在数列
在数列![]() 中,取
中,取![]() ,则
,则![]() ,不满足条件
,不满足条件![]() ,
,
所以数列![]() 不具有“m性质”;
不具有“m性质”;
在数列![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,所以满足条件
,所以满足条件![]() ;
;
![]() (
(![]() )满足条件
)满足条件![]() ,所以数列
,所以数列![]() 具有“性质m”
具有“性质m”
![]() 因为数列
因为数列![]() 是各项为正数的等比数列,则公比
是各项为正数的等比数列,则公比![]() ,
,
将![]() 代入
代入![]() 得,
得,![]() ,
,
解得![]() 或
或![]() 舍去
舍去
所以![]() ,
,![]() ,
,
![]()
对于任意的![]() ,
,![]() ,且
,且![]()
所以数列数列![]() 具有“m性质”
具有“m性质”
且![]()
![]() 由于
由于![]() ,则
,则![]() ,
,![]() ,
,
由于任意![]() 且
且![]() ,数列
,数列![]() 具有“性质m”,所以
具有“性质m”,所以![]()
即![]() ,化简得,
,化简得,![]()
即![]() 对于任意
对于任意![]() 且
且![]() 恒成立,所以
恒成立,所以![]()
![]() 由于
由于![]() 及
及![]() ,所以
,所以![]()
即![]() 时,数列
时,数列![]() 是单调递增数列,且
是单调递增数列,且![]()
只需![]() ,解得
,解得![]()
由![]() 得
得![]() ,所以满足条件的整数t的值为2和3.
,所以满足条件的整数t的值为2和3.
经检验![]() 不合题意,舍去,满足条件的整数只有
不合题意,舍去,满足条件的整数只有![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-![]() x3+2x2+2x,若存在满足0≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
x3+2x2+2x,若存在满足0≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
A. [6,+∞)B. (-∞,2]
C. [2,6]D. [5,6]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是双曲线
是双曲线![]() :
:![]() (
(![]() ,
,![]() )的两个顶点,点
)的两个顶点,点![]() 是双曲线上异于
是双曲线上异于![]() 、
、![]() 的一点,
的一点,![]() 为坐标原点,射线
为坐标原点,射线![]() 交椭圆
交椭圆![]() :
:![]() 于点
于点![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)若双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,且过点
,且过点![]() ,求
,求![]() 的方程;
的方程;
(2)在(1)的条件下,如果![]() ,求△
,求△![]() 的面积;
的面积;
(3)试问:![]() 是否为定值?如果是,请求出此定值;如果不是,请说明理由.
是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,底面ABCD四边长为1的菱形,∠ABC=![]() ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
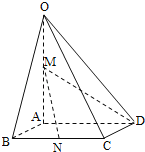
(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小;
(3)求点B到平面OCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是双曲线
是双曲线![]() 的两个顶点,点
的两个顶点,点![]() 是双曲线上异于
是双曲线上异于![]() 、
、![]() 的一点,
的一点,![]() 为坐标原点,射线
为坐标原点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)若双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,且过点
,且过点![]() ,求
,求![]() 的方程;
的方程;
(2)在(1)的条件下,如果![]() ,求
,求![]() 的面积;
的面积;
(3)试问:![]() 是否为定值?如果是,请求出此定值;如果不是,请说明理由.
是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是
是![]() 的两个非空子集,如果存在一个函数
的两个非空子集,如果存在一个函数![]() 满足:①
满足:① ![]() ;② 对任意
;② 对任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,那么称这两个集合为“
,那么称这两个集合为“![]() 到
到![]() 的保序同构”,以下集合对不是“
的保序同构”,以下集合对不是“![]() 到
到![]() 的保序同构”的是( )
的保序同构”的是( )
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数![]() 满足不等式
满足不等式![]() ;
;
命题q:关于![]() 不等式
不等式![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的为( )
A. 由金、银、铜、铁可导电,猜想:金属都可导电
B. 猜想数列![]() 的通项公式为
的通项公式为![]()
C. 半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]()
D. 由平面直角坐标系中圆的方程为![]() ,推测空间直角坐标系中球的方程为
,推测空间直角坐标系中球的方程为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com