解:(Ⅰ)显然函数f(x)的定义域为(0,+∞).
当m=2时,f'(x)=

.
∴当x∈(0,1)时,f'(x)<0,x∈(1,+∞)时,f'(x)>0.
∴f(x)在x=1时取得最小值,其最小值为f(1)=

.(4分)
(Ⅱ)∵f'(x)=x-

+(m-1)=
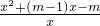
=
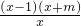
,
∴(1)当-1<m≤0时,若x∈(0,-m)时,f'(x)>0,f(x)为增函数;
当x∈(-m,1)时,f'(x)<0,f(x)为减函数;
x∈(1,+∞)时,f'(x)>0,f(x)为增函数.
(2)当m≤-1时,x∈(0,1)时,f'(x)>0,f(x)为增函数;
x∈(1,-m)时,f'(x)<0,f(x)为减函数;
x∈(-m,+∞)时,f'(x)>0,f(x)为增函数.(9分)
(Ⅲ)当m=-1时,函数f(x)=

+lnx-2x.
构造辅助函数g(x)=f(x)+x,并求导得
g'(x)=x+

-1=
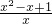
=
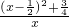
.
∴g'(x)>0,g(x)为增函数.
∴对任意0<x
1<x
2,都有g(x
1)<g(x
2)成立,
即f(x
1)+x
1<f(x
2)+x
2.
即f(x
1)-f(x
2)>x
1-x
2.
又∵x
1-x
2<0,
∴

>-1.(14分)
分析:(I)将m=2代入,我们易求出其导函数f'(x)的解析式,进而易判断基单调性,结合其定义域和单调性,易得到函数f(x)的最小值.
(II)由f'(x)=
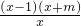
,结合m≤0,我们可以分-1<m≤0与m≤-1两种情况进行分类讨论,利用导数法,讨论函数f(x)的单调性;
(III)当m=-1时,函数f(x)=

+lnx-2x.要证明

>-1,即证明f(x
1)-f(x
2)>x
1-x
2,即证f(x
1)+x
1<f(x
2)+x
2,故我们可以构造辅助函数g(x)=f(x)+x,通过讨论辅助函数g(x)=f(x)+x的单调性证明结论.
点评:本题考查的知识点是利用导数求函数的最值,利用导数研究函数的单调性,利用导数证明函数的单调性是我们证明函数单调性最常的办法,而利用单调性解不等式又是解不等式重要思路.

 x2-mlnx+(m-1)x,其中m∈R.
x2-mlnx+(m-1)x,其中m∈R. >-1.
>-1. .
. .(4分)
.(4分) +(m-1)=
+(m-1)=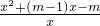 =
=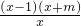 ,
, +lnx-2x.
+lnx-2x. -1=
-1=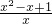 =
=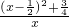 .
. >-1.(14分)
>-1.(14分)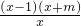 ,结合m≤0,我们可以分-1<m≤0与m≤-1两种情况进行分类讨论,利用导数法,讨论函数f(x)的单调性;
,结合m≤0,我们可以分-1<m≤0与m≤-1两种情况进行分类讨论,利用导数法,讨论函数f(x)的单调性; +lnx-2x.要证明
+lnx-2x.要证明 >-1,即证明f(x1)-f(x2)>x1-x2,即证f(x1)+x1<f(x2)+x2,故我们可以构造辅助函数g(x)=f(x)+x,通过讨论辅助函数g(x)=f(x)+x的单调性证明结论.
>-1,即证明f(x1)-f(x2)>x1-x2,即证f(x1)+x1<f(x2)+x2,故我们可以构造辅助函数g(x)=f(x)+x,通过讨论辅助函数g(x)=f(x)+x的单调性证明结论.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<