
【题目】设a∈R,若x>0时均有[(a﹣1)x﹣1](x2﹣ax﹣1)≥0,则a= .
【答案】![]()
【解析】解:(1)a=1时,代入题中不等式明显不成立.
(2)a≠1,构造函数y1=(a﹣1)x﹣1,y2=x2﹣ax﹣1,它们都过定点P(0,﹣1).
考查函数y1=(a﹣1)x﹣1:令y=0,得M( ![]() ,0),
,0),
∴a>1;
考查函数y2=x2﹣ax﹣1,∵x>0时均有[(a﹣1)x﹣1](x2﹣ax﹣1)≥0,
∴y2=x2﹣ax﹣1过点M( ![]() ,0),代入得:
,0),代入得: ![]() ,
,
解之得:a= ![]() ,或a=0(舍去).
,或a=0(舍去).
所以答案是: ![]() .
.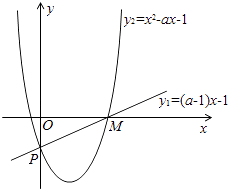
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为An , 第n项之后各项an+1 , an+2…的最小值记为Bn , dn=An﹣Bn .
(1)若{an}为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意n∈N* , an+4=an),写出d1 , d2 , d3 , d4的值;
(2)设d是非负整数,证明:dn=﹣d(n=1,2,3…)的充分必要条件为{an}是公差为d的等差数列;
(3)证明:若a1=2,dn=1(n=1,2,3,…),则{an}的项只能是1或者2,且有无穷多项为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的中学生是否爱好运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 得,
得,![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是 ( )
A. 在犯错误的概率不超过0.001的前提下,认为“爱好运动与性别有关”
B. 在犯错误的概率不超过0.01的前提下,认为 “爱好运动与性别有关”
C. 在犯错误的概率不超过0.001的前提下,认为“爱好运动与性别无关”
D. 有![]() 以上的把握认为“爱好运动与性别无关”
以上的把握认为“爱好运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近日,某地普降暴雨,当地一大型提坝发生了渗水现象,当发现时已有![]() 的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为
的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为![]() 元,且渗水面积以每天
元,且渗水面积以每天![]() 的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积
的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积![]() ,该部门需支出服装补贴费为每人
,该部门需支出服装补贴费为每人![]() 元,劳务费及耗材费为每人每天
元,劳务费及耗材费为每人每天![]() 元.若安排
元.若安排![]() 名人员参与抢修,需要
名人员参与抢修,需要![]() 天完成抢修工作.
天完成抢修工作.
![]() 写出
写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱![]() 。
。

(1)证明FO∥平面CDE;
(2)设BC=![]() CD,证明EO⊥平面CDE。
CD,证明EO⊥平面CDE。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 ![]() ,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分. 
(1)求椭圆C的方程;
(2)求△APB面积取最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小金同学在学校中贯彻着“边玩边学”的学风,他在“汉诺塔”的游戏中发现了数列递推的奥妙:有![]() 、
、![]() 、
、![]() 三个木桩,
三个木桩,![]() 木桩上套有编号分别为
木桩上套有编号分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到
的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到![]() 木桩上,则所需的最少次数为( )
木桩上,则所需的最少次数为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com