
已知函数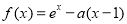 ,其中
,其中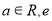 为自然对数底数.
为自然对数底数.
(1)当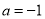 时,求函数
时,求函数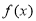 在点
在点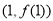 处的切线方程;
处的切线方程;
(2)讨论函数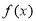 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知 ,若函数
,若函数 对任意
对任意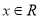 都成立,求
都成立,求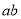 的最大值.
的最大值.
(1)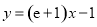 (2)当
(2)当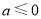 时,函数
时,函数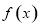 的单调递增区间为
的单调递增区间为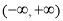 ;当
;当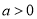 时,函数
时,函数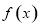 的单调递增区间为
的单调递增区间为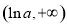 ,单调递减区间为
,单调递减区间为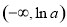 .(3)
.(3)
【解析】
试题分析:(1)根据导数几何意义可求切线斜率: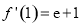 ,再根据点斜式求切线方程为
,再根据点斜式求切线方程为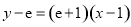 ,即
,即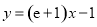 .(2)利用导数求函数单调性,从导函数出发,研究其零点情况:
.(2)利用导数求函数单调性,从导函数出发,研究其零点情况: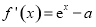 当
当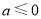 时,
时,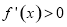 ,无零点,函数
,无零点,函数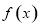 在
在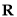 上单调递增;当
上单调递增;当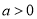 时,由
时,由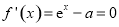 得
得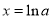 ,
,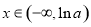 时,
时,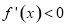 ,
,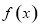 单调递减;
单调递减; 时,
时,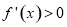 ,
,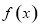 单调递增.(3)不等式恒成立问题转化为函数最值问题:
单调递增.(3)不等式恒成立问题转化为函数最值问题: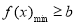 ,当
,当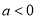 时,函数
时,函数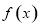 无最小值;当
无最小值;当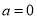 时,函数
时,函数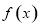 最小值为0,
最小值为0,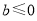 ,此时
,此时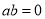 ;当
;当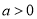 时,
时,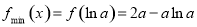 ,
,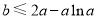 ,
,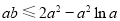 ,最后研究函数
,最后研究函数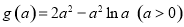 最大值
最大值
试题解析:【解析】
(1)当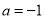 时,
时,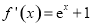 ,
,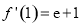 ,
, , 2分
, 2分
∴函数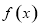 在点
在点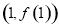 处的切线方程为
处的切线方程为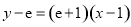 ,
,
即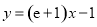 . 4分
. 4分
(2)∵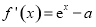 ,
,
①当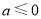 时,
时,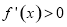 ,函数
,函数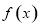 在
在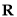 上单调递增; 6分
上单调递增; 6分
②当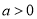 时,由
时,由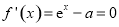 得
得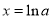 ,
,
∴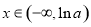 时,
时,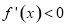 ,
,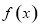 单调递减;
单调递减; 时,
时,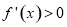 ,
,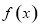 单调递增.
单调递增.
综上,当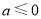 时,函数
时,函数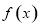 的单调递增区间为
的单调递增区间为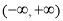 ;当
;当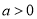 时,函数
时,函数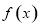 的单调递增区间为
的单调递增区间为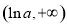 ,单调递减区间为
,单调递减区间为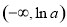 . 9分
. 9分
(3)由(2)知,当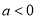 时,函数
时,函数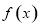 在
在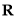 上单调递增,
上单调递增,
∴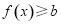 不可能恒成立; 10分
不可能恒成立; 10分
当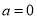 时,
时,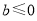 ,此时
,此时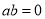 ; 11分
; 11分
当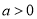 时,由函数
时,由函数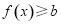 对任意
对任意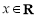 都成立,得
都成立,得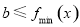 ,
,
∵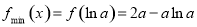 ,∴
,∴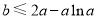 13分
13分
∴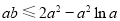 ,
,
设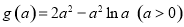 ,∴
,∴ 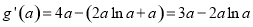 ,
,
由于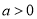 ,令
,令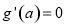 ,得
,得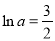 ,
,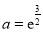 ,
,
当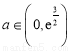 时,
时,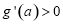 ,
,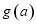 单调递增;
单调递增; 时,
时,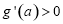 ,
,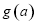 单调递减.
单调递减.
∴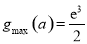 ,即
,即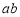 的最大值为
的最大值为 ,
,
此时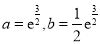 . 16分
. 16分
考点:导数几何意义,利用导数求函数单调性,利用导数求函数最值
考点分析: 考点1:导数及其应用 试题属性

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:2014-2015学年江苏省扬州市高三上学期期末理科数学试卷(解析版) 题型:解答题
射击测试有两种方案,方案1:先在甲靶射击一次,以后都在乙靶射击;方案2:始终在乙靶射击,某射手命中甲靶的概率为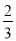 ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为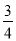 ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量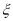 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果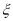 的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
(1)如果该射手选择方案1,求其测试结束后所得分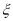 的分布列和数学期望E
的分布列和数学期望E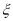 ;
;
(2)该射手选择哪种方案通过测试的可能性大?请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
若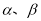 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线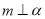 ,则在平面
,则在平面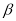 内,一定不存在与直线
内,一定不存在与直线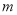 平行的直线.
平行的直线.
②若直线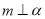 ,则在平面
,则在平面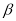 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线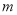 垂直.
垂直.
③若直线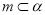 ,则在平面
,则在平面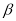 内,不一定存在与直线
内,不一定存在与直线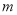 垂直的直线.
垂直的直线.
④若直线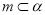 ,则在平面
,则在平面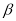 内,一定存在与直线
内,一定存在与直线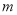 垂直的直线.
垂直的直线.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
已知在全体样本中随机抽取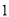 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为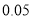
(1)现用分层抽样的方法在所有参与调查的人中抽取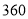 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)已知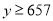 ,
, ,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com