
【题目】设函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数![]() 的单调性.
的单调性.
【答案】(Ⅰ)![]() ;(Ⅱ)讨论见解析
;(Ⅱ)讨论见解析
【解析】
(Ⅰ)利用导数的几何意义求解即可;
(Ⅱ)分类讨论参数![]() 的范围,利用导数证明单调性即可.
的范围,利用导数证明单调性即可.
解:(Ⅰ)当![]() 时,
时,![]()
所以![]() .
.
所以![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)因为![]() ,
,
所以![]() .
.
(1)当![]() 时,因为
时,因为![]()
由![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,
所以![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.
(2)当![]() 时,令
时,令![]() ,得
,得![]() .
.
① 当![]() 时,
时,
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() 或
或![]() .
.
所以![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 和
和![]() 内单调递减.
内单调递减.
②当![]() 时,
时,
由![]() 得
得![]() 或
或![]() ;
;
由![]() 得
得![]() .
.
所以![]() 在区间
在区间![]() 和
和![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.
③当![]() 时,因为
时,因为![]()
所以![]() 在区间
在区间![]() 内单调递增.
内单调递增.
④当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ;
;
由![]() 得
得![]() .
.
所以![]() 在区间
在区间![]() 和
和![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.
综上可知,当![]() 时,
时,![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减;
内单调递减;
当![]() 时,
时,![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 和
和![]() 内单调递减;
内单调递减;
当![]() 时,
时,![]() 在区间
在区间![]() 和
和![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减;
内单调递减;
当![]() 时,
时,![]() 在区间
在区间![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() 在区间
在区间![]() 和
和![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.


科目:高中数学 来源: 题型:
【题目】以下四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的充分不必要条件; ③若
”的充分不必要条件; ③若![]() 为假命题,则
为假命题,则![]() 均为假命题;④对于命题
均为假命题;④对于命题![]() 使得
使得![]() ,则
,则![]() 为
为![]() ,均有
,均有![]() .其中,真命题的个数是 ( )
.其中,真命题的个数是 ( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应新高考改革,某校组织了一次新高考质量测评(总分100分),在成绩统计分析中,抽取12名学生的成绩以茎叶图形式表示如图,学校规定测试成绩低于87分的为“未达标”,分数不低于87分的为“达标”.
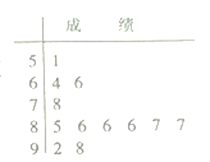
(1)求这组数据的众数和平均数;
(2)在这12名学生中从测试成绩介于80~90之间的学生中任选2人,求至少有1人“达标”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 的上顶点,
的上顶点,![]() ,且
,且![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() ,求当
,求当![]() 的面积取得最大值时,直线
的面积取得最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆方程为![]() ,过点
,过点![]() 的直线l交椭圆于点A,B,O是坐标原点,点P满足
的直线l交椭圆于点A,B,O是坐标原点,点P满足![]() ,点N的坐标为
,点N的坐标为![]() ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)![]() 的最小值与最大值.
的最小值与最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
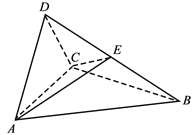
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
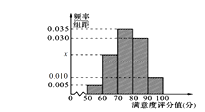
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
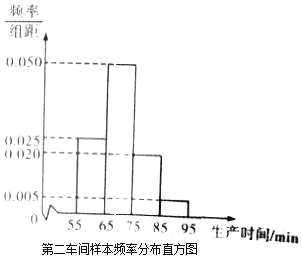
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中随机抽取2人,求抽取的2人中,至少1人生产时间小于65min的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com