
【题目】如图所示, 四棱锥![]() 底面是直角梯形,
底面是直角梯形, ![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
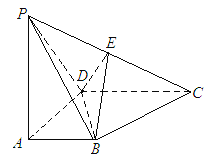
(Ⅰ)证明: ![]() ;
;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+1,x∈N*.若x0,n∈N*,使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0,n)为函数f(x)的一个“生成点”.则函数f(x)的“生成点”共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆C: ![]() 的离心率为
的离心率为![]() ,右焦点为(
,右焦点为(![]() ,0).(1)求椭圆C的方程;(2)若过原点
,0).(1)求椭圆C的方程;(2)若过原点![]() 作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求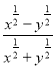 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三一次月考之后,为了为解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成了下面频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 5 | 0.05 |
第二组 |
| 35 | 0.35 |
第三组 |
| 30 | 0.30 |
第四组 |
| 20 | 0.20 |
第五组 |
| 10 | 0.10 |
合计 | 100 | 1.00 | |
(1)试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在![]() 中的学生数为
中的学生数为![]() ,
,
求:①在三次抽取过程中至少有两次连续抽中成绩在![]() 中的概率;
中的概率;
②![]() 的分布列和数学期望.(注:本小题结果用分数表示)
的分布列和数学期望.(注:本小题结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com