
| A. | 216 | B. | 72 | C. | 144 | D. | 288 |
分析 利用间接法,除歌曲外,先排列没有限制的排列,再排除魔术节目和相声节目相邻或和小品节目相邻的,还要加上魔术节目既和相声节目相邻且和小品节目相邻的,问题得以解决.
解答 解:利用间接法,除歌曲外,没有限制的排列有${A}_{6}^{6}$,再排除魔术节目和相声节目相邻或和小品节目相邻的有2${A}_{2}^{2}•{A}_{5}^{5}$,还要加上魔术节目既和相声节目相邻且和小品节目相邻的有${A}_{2}^{2}•{A}_{4}^{4}$,故不同的表演顺序的种数为${A}_{6}^{6}$-2${A}_{2}^{2}•{A}_{5}^{5}$+${A}_{2}^{2}•{A}_{4}^{4}$=288种,
故选:D.
点评 本题考查计数原理的应用,考查学生分析解决问题的能力,比较基础


科目:高中数学 来源: 题型:解答题
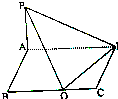 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a>1,b>0 | B. | a>1,b<0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com