
分析 (1)利用递推式、等比数列的通项公式即可得出;
(2)利用“错位相减法”、等差数列与等比数列前n项和公式即可得出.
解答 (1)证明:∵Sn=2an+n-3成立,
∴当n=1时,a1=2a1+1-3,解得a1=2.
当n≥2时,Sn-1=2an-1+n-1-3,
an=2an-2an-1+1,化为an=2an-1-1,变形为an-1=2(an-1-1),
∴数列{an-1}为等比数列,首项为a1-1=1,公比为2;
(2)解:由(1)可得:${a}_{n}-1=1×{2}^{n-1}$,
∴${a}_{n}={2}^{n-1}+1$.
∴$n{a}_{n}=n({2}^{n-1}+1)$=n•2n-1+n.
设An=1+2×2+3×22+…+n×2n-1,
∴2An=2+2×22+3×23+…+(n-1)×2n-1+n×2n,
∴-An=1+2+22+…+2n-1-n×2n=2$\frac{{2}^{n}-1}{2-1}$-n×2n=(1-n)×2n-1,
∴An=(n-1)×2n+1,
∴数列{nan}的前n项和Tn=(n-1)×2n+1+$\frac{n(n+1)}{2}$.
点评 本题考查了递推式的应用、“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
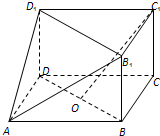 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 216 | B. | 72 | C. | 144 | D. | 288 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 10 | 20 | 30 | 40 | 50 | 60 |
| y | 39 | 28 | m | n | 43 | 41 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com