
分析 (1)利用生产这种产品的固定成本为60000元,变成成本为每件20元,最低产量为10000件,可得总成本函数;
(2)产量为x件,则可降价的次数为$\frac{x-10000}{2000}$,可得收益函数;
(3)利润函数=收益函数R(x)-总成本函数C(x).
解答 解:(1)设产量为x件,那么x≥10000,则总成本函数C(x)=60000+20x;
(2)产量为x件,则可降价的次数为$\frac{x-10000}{2000}$,收益函数R(x)=x(50-$\frac{x-10000}{2000}$×2)=x(60-$\frac{x}{1000}$);
(3)利润函数L(x)=x(60-$\frac{x}{1000}$)-(60000+20x)=-$\frac{{x}^{2}}{1000}$+40x-60000.
点评 本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,比较基础.


科目:高中数学 来源: 题型:解答题
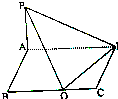 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a>1,b>0 | B. | a>1,b<0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com