Question

20．某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据：

x	2	4	5	6	8
y	30	40	60	50	70

（1）画出散点图；
（2）求回归直线方程；
（3）据此估计广告费用为12万元时，销售收入y的值．
附：线性回归方程：$\stackrel{∧}{y}$=bx+a，其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{{x}^{2}}-{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$．

Answer 1

分析 （1）根据所给的数据，写出5组坐标，作出散点图如图所示．
（2）根据所给的数据先做出横标和纵标的平均数，利用最小二乘法写出线性回归方程系数的表达式，把样本中心点代入求出a的值，得到线性回归方程．
（3）根据所给的变量x的值，把值代入线性回归方程，得到对应的y的值，这里的y的值是一个预报值．

解答 解：（1）根据所给的数据，写出5组坐标，作出散点图如图所示：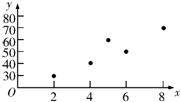
…（2分）
（2）求回归直线方程．
$\overline{x}$=$\frac{1}{5}$（2+4+5+6+8）=5，$\overline{y}$=$\frac{1}{5}$（30+40+60+50+70）=50_…4分
$\sum _{i=1}^{5}$${x}_{i}^{2}$=145，
$\sum _{i=1}^{5}$x_iy_i=1380，…6 分
b=$\frac{\sum _{i=1}^{5}{x}_{i}{y}_{i}-5\overline{x}\overline{y}}{\sum _{i=1}^{5}{{x}_{i}}^{2}-5{\overline{x}}^{2}}$=$\frac{1380-5×5×50}{145-5×{5}^{2}}$=6.5，
a=50-6.5×5=17.5
∴因此回归直线方程为y=6.5x+17.5；_…10分
（3）当x=12时，预报y的值为y=12×6.5+17.5=95.5万元． 
即广告费用为12万元时，销售收入y的值大约是95.5万元．…（12分）

点评 本题考查线性回归方程的求法和应用，本题解题的关键是求出线性回归方程的系数，这是后面解题的先决条件．