
分析 (1)作OD⊥AB于D,当k=$\frac{\sqrt{2}}{2}$时,直线l:y=$\frac{\sqrt{2}}{2}$x+2,求出|AB|,|OD|,即可求出S的值;
(2)设∠AOB=θ(0θ<180°),则S=$\frac{1}{2}$|OA||OB|sinθ=2sinθ,即可求S的最大值,从而求出此时的k值.
解答 解:(1)作OD⊥AB于D,当k=$\frac{\sqrt{2}}{2}$时,直线l:y=$\frac{\sqrt{2}}{2}$x+2,则|OD|=$\frac{2}{\sqrt{1+\frac{1}{2}}}$=$\frac{2\sqrt{6}}{3}$,…(2分)
|AB|=2$\sqrt{4-\frac{8}{3}}$=$\frac{4\sqrt{3}}{3}$,…(4分)
∴S=$\frac{1}{2}$|AB||OD|=$\frac{4\sqrt{2}}{3}$;…(6分)
(2)设∠AOB=θ(0θ<180°)
则S=$\frac{1}{2}$|OA||OB|sinθ=2sinθ,…(8分)
∴当θ=90°时,S(θ)max=2,此时|OD|=$\sqrt{2}$,…(10分)
即$\frac{2\sqrt{2}|k|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,
∴k=±$\frac{\sqrt{3}}{3}$.…(12分)
点评 本题考查直线与圆的位置关系,点到直线的距离,三角形面积公式的应用,考查计算能力.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:解答题
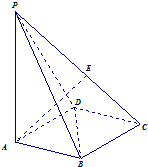 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知A(x1,y1)为抛物线y2=2px(p>0)上的动点,P(p,0)为定点.
如图,已知A(x1,y1)为抛物线y2=2px(p>0)上的动点,P(p,0)为定点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{3}+4}}{10}$ | B. | $\frac{{3\sqrt{3}-4}}{10}$ | C. | $\frac{{4-3\sqrt{3}}}{10}$ | D. | $-\frac{{3\sqrt{3}+4}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π^2}{8}+1$ | B. | $\frac{π^2}{4}+2$ | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com