
设函数f(x)=sin(2x+φ)(﹣π<φ<0),y=f(x)图象的一条对称轴是直线 .
.
(I)求φ,并指出y=f(x)由y=sin2x作怎样变换所得.
(II)求函数y=f(x)的单调增区间;
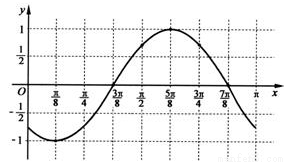
(III)画出函数y=f(x)在区间[0,π]上的图象.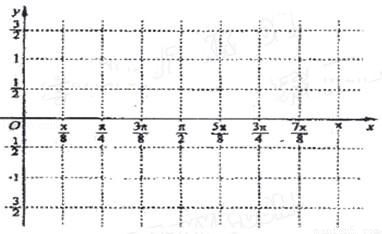
(1)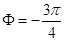 右移
右移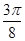 个单位 (2)
个单位 (2)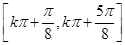 (3)略
(3)略
【解析】
试题分析:(1)因为函数f(x)=sin(2x+φ)在对称轴时有最大或最小值,据此就可得到含?的等式,求出?值.因为x=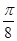 是函数y=f(x)的图象的对称轴,所以sin(2×
是函数y=f(x)的图象的对称轴,所以sin(2×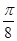 +?)=±1,即
+?)=±1,即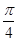 +?=kπ+
+?=kπ+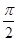 ,k∈Z.因为-π<φ<0,所以?=-
,k∈Z.因为-π<φ<0,所以?=-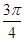 .
.
(2)借助基本正弦函数的单调性来解,因为y=sinx在区间[2kπ- 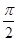 ,2kπ+
,2kπ+ 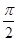 ],k∈Z上为增函数,所以只需2x-
],k∈Z上为增函数,所以只需2x-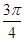 ∈[2kπ-
∈[2kπ- 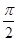 ,2kπ+
,2kπ+ 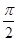 ],k∈Z,在解出x的范围
],k∈Z,在解出x的范围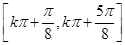 即可.
即可.
(3)利用五点法作图,令x分别取0,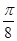 ,
,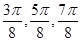 ,π,求出相应的y值,就可得到函数在区间[0,π]上的点的坐标,再把坐标表示到直角坐标系,用平滑的曲线连接即可得到所求图象。
,π,求出相应的y值,就可得到函数在区间[0,π]上的点的坐标,再把坐标表示到直角坐标系,用平滑的曲线连接即可得到所求图象。
考点:三角函数的性质
点评:本小题主要考查根据三角函数的性质求解析式,以及单调区间,三角函数图象的画法,考查学生的推理和运算能力


科目:高中数学 来源: 题型:
| π | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| ||
| 3 |
| ||
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com