
【题目】定义区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度为
的长度为![]() .如果一个函数的所有单调递增区间的长度之和为
.如果一个函数的所有单调递增区间的长度之和为![]() (其中
(其中![]() ,
,![]() 为自然对数的底数),那么称这个函数为“
为自然对数的底数),那么称这个函数为“![]() 函数”.下列四个命题:
函数”.下列四个命题:
①函数![]() 不是“
不是“![]() 函数”;
函数”;
②函数![]() 是“
是“![]() 函数”,且
函数”,且![]() ;
;
③函数![]() 是“
是“![]() 函数”;
函数”;
④函数![]() 是“
是“![]() 函数”,且
函数”,且![]() .
.
其中正确的命题的个数为( )
A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
利用导数、函数的图象,对四个命题逐一判断出真假。
分析命题①: ![]() 定义域为
定义域为![]() ,
,![]() ,
,
![]() ,
,![]() 函数
函数![]() 在
在![]() 上是单调递增,显然这个区间没有长度,因此函数
上是单调递增,显然这个区间没有长度,因此函数![]() 不是“
不是“![]() 函数”,故命题①是真命题。
函数”,故命题①是真命题。
分析命题②:![]() ,定义域为
,定义域为![]() ,
, ![]()
当![]() 时,函数
时,函数![]() 是增函数,
是增函数,![]()
![]()
![]()
构造两个函数,![]() ,图象如下图所示:
,图象如下图所示:

通过图象可知当![]() ,
,![]() 而
而![]() ,即
,即![]() ,
, ![]() ,所以当
,所以当![]() 时,函数
时,函数![]() 是增函数,增区间的长度为
是增函数,增区间的长度为![]() ,又因为
,又因为![]() 显然有
显然有![]() 成立,所以函数
成立,所以函数![]() 是“m函数”,
是“m函数”,![]()
![]()
![]()
![]() 即
即![]() 成立,故命题②是真命题。
成立,故命题②是真命题。
分析命题③: 函数![]() 定义域为
定义域为![]() ,
,![]()
显然![]() 时,
时,![]() ,此时函数
,此时函数![]() 是单调递增函数,增区间为
是单调递增函数,增区间为![]() ,而区间
,而区间![]() 没有长度,故函数
没有长度,故函数![]() 不是“
不是“![]() 函数”,故命题③是假命题。
函数”,故命题③是假命题。
分析命题④:函数![]() 定义域
定义域![]() ,
,![]()
当![]() 时,
时,![]() 是增函数,故只需
是增函数,故只需![]() 成立,
成立,![]() 是增函数,
是增函数,
也就是![]() 成立,
成立,![]() 是增函数,构造二个函数,
是增函数,构造二个函数,![]() 如下图所示:
如下图所示:
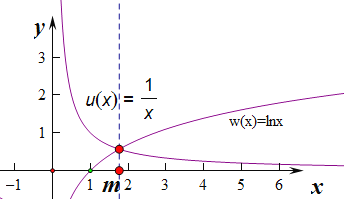
通过图象可知:当![]() 时,
时,![]() ,而
,而![]() ,所以
,所以![]() 。从而有
。从而有![]() 时,
时,![]() 时,函数
时,函数![]() 是增函数,显然区间
是增函数,显然区间![]() 长度为
长度为![]() ,而
,而![]()
所以函数![]() 是“
是“![]() 函数”,又
函数”,又![]() ,即
,即![]() 。故命题④是真命题。
。故命题④是真命题。
综上所述:正确的命题的个数为3个,故本题选B。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为![]() ,且过点
,且过点![]() .点M(3,m)在双曲线上.
.点M(3,m)在双曲线上.
(1)求双曲线的方程;
(2)求证:![]() ;
;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭园C:
分别是椭园C:![]() 的左、右焦点,且椭圆C上的点到
的左、右焦点,且椭圆C上的点到![]() 的距离的最小值为
的距离的最小值为![]() ,点M,N是椭圆C上位于x轴上方的两点,且向量
,点M,N是椭圆C上位于x轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 当
当![]() 时,求
时,求![]() 的面积;
的面积;
![]() 当
当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心为坐标原点,焦点在坐标轴上,且经过点M(4,1),N(2,2).
(1)求椭圆C的方程;
(2)若斜率为1的直线与椭圆C交于不同的两点,且点M到直线l的距离为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B,C是三个事件,给出下列四个事件:
(Ⅰ)A,B,C中至少有一个发生;
(Ⅱ)A,B,C中最多有一个发生;
(Ⅲ)A,B,C中至少有两个发生;
(Ⅳ)A,B,C最多有两个发生;
其中相互为对立事件的是( )
A.Ⅰ和ⅡB.Ⅱ和ⅢC.Ⅲ和ⅣD.Ⅳ和Ⅰ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】老况、老王、老顾、小周、小郭和两位王女士共7人要排成一排拍散伙纪念照.
(1)若两位王女士必须相邻,则共有多少种排队种数?
(2)若老王与老况不能相邻,则共有多少种排队种数?
(3)若两位王女士必须相邻,若老王与老况不能相邻,小郭与小周不能相邻,则共有多少种排队种数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点E到点A(2,0)与点B(-2,0)的直线斜率之积为-![]() ,点E的轨迹为曲线C.
,点E的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点D(l,0)作直线l与曲线C交于P,Q两点,且![]() =-
=-![]() .求直线l的方程.
.求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (为参数,倾斜角),曲线C的参数方程为
(为参数,倾斜角),曲线C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系。
轴正半轴为极轴建立极坐标系。
(1)写出曲线![]() 的普通方程和直线的极坐标方程;
的普通方程和直线的极坐标方程;
(2)若直线与曲线![]() 恰有一个公共点
恰有一个公共点![]() ,求点
,求点![]() 的极坐标。
的极坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com