
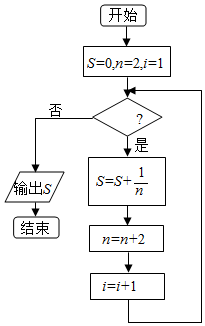
 如图,给出的是求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{30}$的值的一个程序框图,则判断框内填入的条件是( )
如图,给出的是求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{30}$的值的一个程序框图,则判断框内填入的条件是( )| A. | i≥15 | B. | i≤15 | C. | i≥14 | D. | i≤14 |
分析 由已知中程序的功能是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{30}$的值,根据已知中的程序框图,我们易分析出进行循环体的条件,进而得到答案.
解答 解:模拟程序的运行,可知程序的功能是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{30}$的值,
即n≤30,i≤15时,进入循环,当i=16时,退出循环,
则判断框内填入的条件是i≤15.
故选:B.
点评 本题考查的知识点是循环结构的程序框图的应用,解答本题的关键是根据程序的功能判断出最后一次进入循环的条件,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
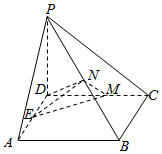 如图,已知四棱锥P-ABCD中,底面ABCD是矩形,PD=AB=2AD=2,PC=2$\sqrt{2}$,M,N分别是CD,PB的中点,
如图,已知四棱锥P-ABCD中,底面ABCD是矩形,PD=AB=2AD=2,PC=2$\sqrt{2}$,M,N分别是CD,PB的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1} | B. | {x|x>1} | C. | {x|x<-1或x>1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
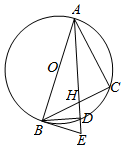 如图,圆O的直径为AB且BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
如图,圆O的直径为AB且BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 1或-3 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
| 1 40 2 44 3 40 4 41 5 33 6 40 7 45 8 42 9 43 | 10 36 11 31 12 38 13 39 14 43 15 45 16 39 17 38 18 36 | 19 27 20 43 21 41 22 37 23 34 24 42 25 37 26 44 27 42 | 28 34 29 39 30 43 31 38 32 42 33 53 34 37 35 49 36 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com