
分析 利用还是偶函数,利用三角函数的基本关系式,化简所求的表达式,换元法令t=sinx+cosx,通过二次函数的性质,从而求函数的最值.
解答 解:函数f(x)=x2+(a2+b2-9)x+a+b+ab为偶函数,可得a2+b2=9,
函数的图象与y轴交点的纵坐标为:a+b+ab,令a=3sinx,b=3cosx,
a+b+ab=3sinx+3cosx+9sinxcosx,
令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
则-$\sqrt{2}$≤t≤$\sqrt{2}$,t2=1+2sinxcosx,
则sinxcosx=$\frac{{t}^{2}-1}{2}$,
则f(x)=3sinx+3cosx+9sinxcosx
=3t+9$\frac{{t}^{2}-1}{2}$=$\frac{9}{2}$(t2+$\frac{2}{3}$t-1)
=$\frac{9}{2}$(t+$\frac{1}{3}$)2-5;
∵-$\sqrt{2}$≤t≤$\sqrt{2}$,
∴-5≤$\frac{9}{2}$(t+$\frac{1}{3}$)2-5≤$3\sqrt{2}+\frac{9}{4}$;
故函数的图象与y轴交点的纵坐标的最大值与最小值:3$\sqrt{2}$-$\frac{11}{4}$.
故答案为:3$\sqrt{2}$-$\frac{11}{4}$.
点评 本题考查了换元法与配方法求函数的值域,考查转化思想的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
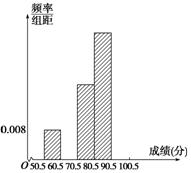 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.4 | B. | 3.0 | C. | 3.6 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±2x | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com