
【题目】在直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线l与曲线C交于不同的两点A,B.
,直线l与曲线C交于不同的两点A,B.
(1)求曲线C的参数方程;
(2)若点P为直线与x轴的交点,求![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,双曲线![]() 的渐近线与抛物线
的渐近线与抛物线![]() 交于点O,A,B,且
交于点O,A,B,且![]() 的垂心为
的垂心为![]() 的焦点,则
的焦点,则![]() 的离心率为______;如果
的离心率为______;如果![]() 与
与![]() 在第一象限内有且只有一个公共点,且
在第一象限内有且只有一个公共点,且![]() ,那么
,那么![]() 的方程为____________.
的方程为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为9,最小值为1,记
上的最大值为9,最小值为1,记![]() ;
;
(1)求实数![]()
![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,其中
,其中![]()
![]()
![]()
![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,如果存在一个常数
个小区间,如果存在一个常数![]() ,使得和式
,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数,试判断函数
上的有界变差函数,试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由.
的最小值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生的选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了解高一年级![]() 名学生选考科目的意向,随机选取
名学生选考科目的意向,随机选取![]() 名学生进行了一次调查,统计选考科目人数如下表:
名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
| |
女生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
|
(1)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(2)假设男生、女生选择选考科目是相互独立的.从选考方案确定的![]() 名学生中随机选出
名学生中随机选出![]() 名,试求在选取的
名,试求在选取的![]() 名学生中恰有
名学生中恰有![]() 名男生的条件下两名学生的选考方案中都含有历史学科的概率;
名男生的条件下两名学生的选考方案中都含有历史学科的概率;
(3)从选考方案确定的![]() 名男生中随机选出
名男生中随机选出![]() 名,设随机变量
名,设随机变量![]() 表示所选
表示所选![]() 人中选考方案完全相同的人数(若有
人中选考方案完全相同的人数(若有![]() 组
组![]() 人选考方案完全相同,则
人选考方案完全相同,则![]() ),求
),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形ABCD是直角梯形,
.四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
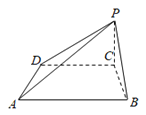
(1)求证:![]() 平面PDC.
平面PDC.
(2)请在图中所给的五个点P,A,B,C,D中找出两个点,使得这两点所在直线与直线BC垂直,并给出证明.
(3)当平面![]() 平面ABCD时,求直线PC与平面PAB所成角的正弦值.
平面ABCD时,求直线PC与平面PAB所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com