
|
A、
| ||
| B、2 | ||
C、
| ||
D、
|
|
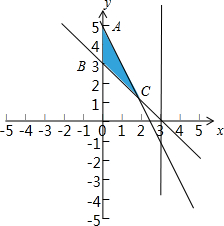 解:不等式组
解:不等式组
|
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
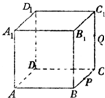 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图为与杨辉三角结构相似的“巴斯卡”三角,这个三角的构造方法是:除第一行为1外,其余各行中的每一个数,都等于它右肩上的数乘以右肩所在的行数,再加上左肩而得.例如第5行第3个数是35,它的右肩为6,左肩为11,右肩所在的行数为4,所以35=6×4+11.这个三角中的数与下面这个展开式中的系数有关:x(x+1)(x+2)…[x+(n-1)]=anxn+an-1xn-1+…+a1x,则在“巴斯卡”三角中,第8行从左到右的第2个数到第7个数之和为( )
如图为与杨辉三角结构相似的“巴斯卡”三角,这个三角的构造方法是:除第一行为1外,其余各行中的每一个数,都等于它右肩上的数乘以右肩所在的行数,再加上左肩而得.例如第5行第3个数是35,它的右肩为6,左肩为11,右肩所在的行数为4,所以35=6×4+11.这个三角中的数与下面这个展开式中的系数有关:x(x+1)(x+2)…[x+(n-1)]=anxn+an-1xn-1+…+a1x,则在“巴斯卡”三角中,第8行从左到右的第2个数到第7个数之和为( )| A、322559 |
| B、35279 |
| C、5880 |
| D、322560 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(57,18) |
| B、(39,3) |
| C、(39,18) |
| D、(21,18) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、4n-4个 | ||
| B、8n-24个 | ||
| C、2n(n-2)个 | ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com